How is mathematics applied to real world problems?
Mathematics is essential to our way of life. It is used all around us, from weather forecasting, engineering and finance to modelling how diseases spread. Professor Anotida Madzvamuse, an applied mathematician at the University of Sussex, in the UK, and the University of British Columbia, in Canada, led the UK-Africa Postgraduate Advanced Study Institute in Mathematical Sciences.
TALK LIKE AN … APPLIED MATHEMATICIAN
Dynamical system — a collection of objects and their interconnections which evolve in time and space
Mathematical modelling — the ability to translate observations (experimental or otherwise) using mathematical theories and laws of physics to represent important features from a real-world problem. Modelling approximates the reality as reality is far too complex to be described. Modelling is used to build understanding of the application area, test a theory or hypothesis, and visualise or predict an outcome
Parameter — a variable that is configurable and defines the specific behaviour of a model. This variable is independent of space and time, and, in many cases, denotes the physical units associated with the dynamical system
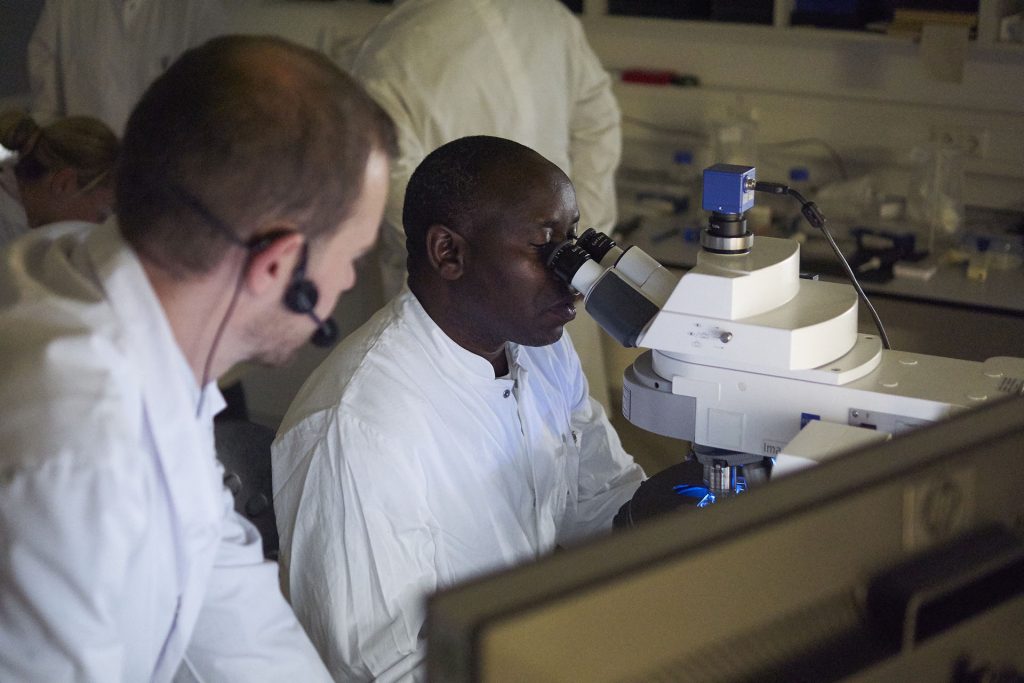
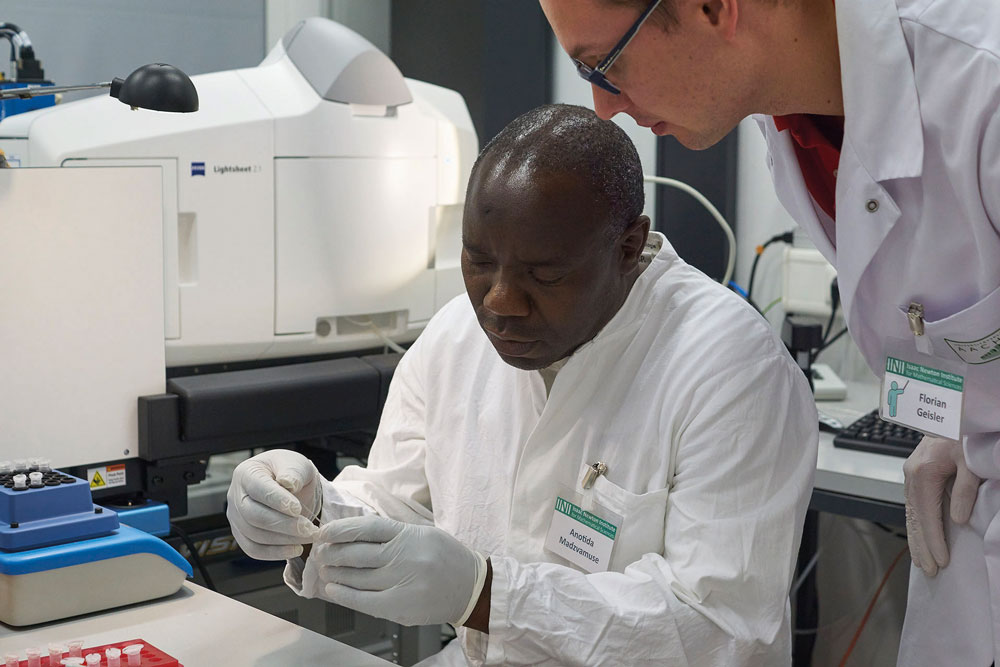
Applied mathematics is the application of mathematics to real world problems. It is an incredibly useful field with a wide range of applications from biological and social sciences to computer animation and finance. Professor Anotida Madzvamuse is a professor of mathematical and computational biology whose work includes data-driven mathematical modelling, mathematical analysis of models, parameter estimation and model selection by fitting models to data. This cyclic modelling approach allows for models to be validated – or invalidated – and enables Anotida to select the models or processes that best describe the applications under study. Passionate about training a new generation of early career scientists, he is the principal investigator for the UK-Africa Postgraduate Advanced Study Institute in Mathematical Sciences (UK-APASI).
Mathematics in the real world
Whilst pure mathematics is about solving problems and developing theories within mathematics, applied mathematics uses those mathematical theories to solve real world problems. Mathematicians can utilise modelling to do this, usually in the form of equations. They then use the models to both help understand the original problem, and to discover new features about it. Modelling is fundamental to much of our understanding of the world. For example, weather forecasts are a well-known example of mathematical modelling.
Mathematics and government decision-making
Using powerful predictive models, mathematicians can provide quantitative solutions which can influence government policies. “Decision making based on the models are rigorously tested and validated as part of our modelling-data approach,” says Anotida. This way, predictions and forecasting are driven by the dynamical systems, which, in turn, are driven by observations. For example, mathematics has been essential to the modelling of COVID-19 for directing government decisions on non-pharmaceutical interventions such as lockdowns. Anotida has worked on predictive models which have been applied innovatively to provide early warning surveillance systems to support the operational management of hospitals and mortuaries. This work was done in collaboration with Dr James Van Yperen (University of Sussex, UK) and Dr Eduard Campillo-Funollet (University of Lancaster, UK), and public health analysts and NHS commissioners from the southeast of the UK.
Data-driven mathematical modelling
Anotida works with non-mathematicians to formulate new mathematics from scratch based on physical observations and principles, which he calls ‘data-driven mathematical modelling’. “Once we have the models, I am interested in the rigorous mathematical analysis of them,” he explains. “Since most of these models are highly complex, nonlinear and in many cases involving many equations (systems), analytical solutions are not readily available.” From here, Anotida and his collaborators develop and implement novel numerical methods to efficiently and accurately solve the models. These approximate solutions are extremely useful to understand the physics of the problem. “A key part of the numerical method is that it must capture the inherent properties of the mathematical formalism, and these could be mass conservation, positivity of solutions, bounded of solutions and many other properties,” says Anotida.
“Many of these models are characterised by parameters that describe, for example in the case of cell migration, biochemical molecular rates and mechanical properties of the physical model,” he explains. Some of these parameters can be measured during observations but many are not obtained through measurements. It is here that mathematics, through statistical modelling, comes to the rescue. Anotida infers these parameters by fitting models to physical data in a statistical sense. This leads to the concept of identifying the best model that describes the physical phenomena. Anotida’s philosophy is to propose various models depending on the biological or physical and mathematical assumptions, rather than a single model.
Applied mathematics in Africa
Applied mathematics is essential to solving real world problems in many areas, and Anotida’s work goes far beyond his own research in theoretical and computational biology. He wants to ensure the next generation of African applied mathematicians has the skills it needs to impact society in a positive way. There have been recent advances in data acquisition across the African continent in infectious diseases, crime, wildlife management, conservation and other areas. This demands new approaches to understanding the dynamics of such datasets and to make predictions that can help practitioners make policies that are based on rigorous scientific studies. However, many junior staff members in university mathematics departments across Sub-Saharan Africa do not possess a PhD, with almost 80% of faculty staff having, at most, a master’s degree. “It is critically important that the next generation of scientists should be able to communicate seamlessly across disciplines to facilitate cross-fertilisation of ideas, techniques and approaches,” says Anotida.
Introducing UK-APASI
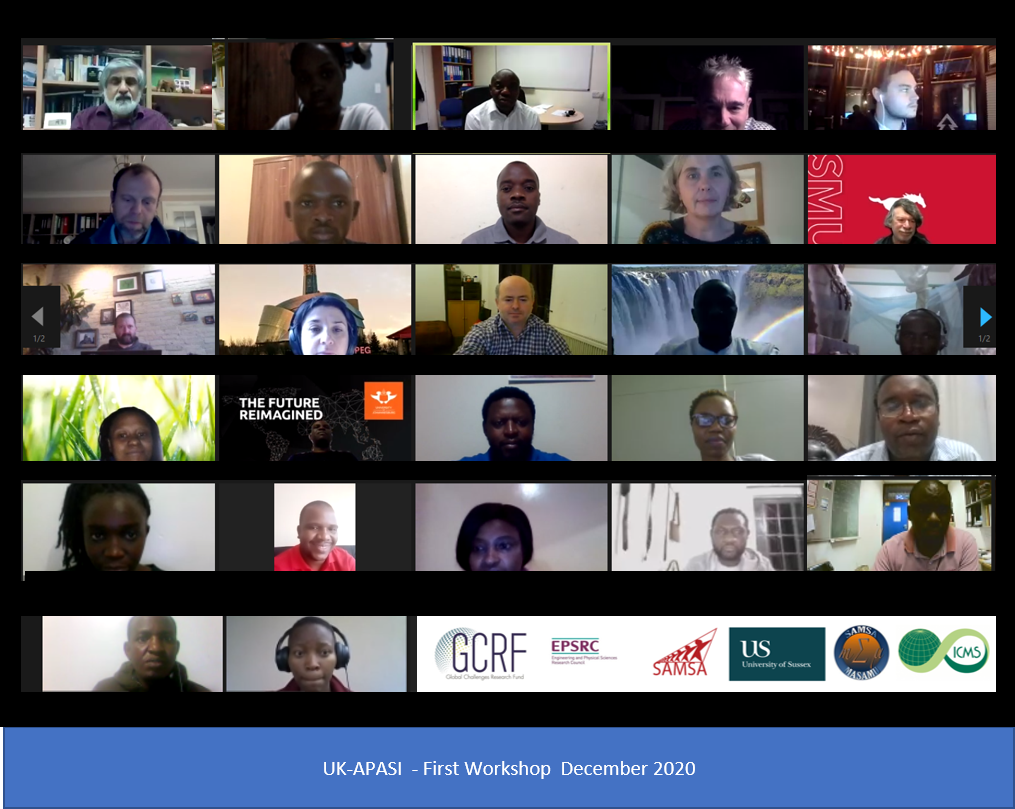
To train and develop such highly skilled mathematicians, Anotida is the principal investigator of the UK-Africa Postgraduate Advanced Study Institute in Mathematical Sciences. This is a research consortium between the UK, Africa and other interested partners which is forging relationships between applied mathematicians in the UK and the Sub-Saharan African region, Europe and North America. The expertise of world-leading international researchers and academics is vital for supporting other continents where such expertise is either non-existent or difficult to access. In particular, knowledge transfer from international applied mathematicians to early career researchers in Africa, while they are resident in their host countries, is key. This benefits both, as established academics develop research projects involving international collaborations, while early career researchers in (or from if they are moving away to host countries) Africa are exposed to world-leading knowledge, techniques and approaches which they can use to address global challenges.
Reference
https://doi.org/10.33424/FUTURUM330
UK-APASI’s Achievements
Around 40 early career African researchers were enrolled in the programme, from Malawi, Nigeria, Kenya, Ghana, South Africa, Botswana, Eswatini, Mozambique and Zimbabwe. The UK-APASI trained them on current state-of-the-art theoretical, statistical, computational and applied techniques in mathematical sciences. The researchers worked on crime modelling, infectious diseases (COVID-19), plant biology (infectious diseases in plants), cell biology (the mechano-biochemical models for cells) and financial mathematics.
The future of UK-APASI
The long-term impact of the programme includes early career African researchers assuming senior academic positions (through promotions and appointments), increased employment in Africa, influencing public policy through science and the creation of new mathematical models and, therefore, new knowledge. The programme was funded for one year and, due to the COVID-19 pandemic, a one-year extension was awarded. Anotida believes it is critically important that long-term funding for such programmes is made available as many early career researchers in Africa were not able to take part due to limited numbers. In particular, Anotida calls for African governments to create funding schemes for training early career researchers. Without such funding, a lot of early career African mathematics researchers are not able to pursue further postgraduate training in applied mathematics while they are resident in their home countries. It is imperative to continue to seek funding from any funding bodies that can support capacity building and human infrastructure training in Africa.
 PROFESSOR ANOTIDA MADZVAMUSE
PROFESSOR ANOTIDA MADZVAMUSE
Department of Mathematics, University of British Colombia, Vancouver, Canada
Previously: School of Mathematical and Physical Sciences, University of Sussex, UK
Fields of research: Mathematical and Computational Biology, Numerical Analysis and HPC Scientific Computing
Research project: Co-ordinating the UK-Africa Postgraduate Advanced Study Institute in Mathematical Sciences (UK-APASI) which supports the training of early career African researchers in applied mathematics
Funders: UKRI/Engineering and Physical Sciences Research Council (EP/T00410X/1), Global Challenges Research Fund, Royal Society, Leverhulme Trust, Health Foundation, National Institute of Health Research, Europe Horizon2020, Brighton and Hove City Council, Isaac Newton Institute for Mathematical Sciences, International Centre for Mathematical Sciences, London Mathematical Society, British Council, Newton Fund, Department of Higher Education and Training in South Africa
ABOUT APPLIED MATHEMATICS
Applied mathematics involves the application of mathematics to solving real world problems. The areas it can be used in are vast, including physical and biological sciences, engineering, social sciences and other diverse fields, from computer animation to finance and economics. Possible job titles that involve applied mathematics include actuary, statistician, scientific programmer, systems engineer, analyst, research associate, teacher and technical consultant. Many applied mathematicians work in academia, teaching the next generation of early career researchers and developing innovations through their own research.
Anotida’s research lies at the interface between fundamental disciplines (mathematics, numerical analysis, physics and scientific computing) and experimental sciences (developmental biology, biochemistry, cell biology, biomedicine and plant biology). He seeks to propose, develop, analyse and simulate new mathematical and computational approaches applied to experimental sciences.
Pathway from school to applied mathematics
• To pursue applied mathematics as a career, Anotida recommends you have a very strong pure and applied
mathematics background and knowledge in numerical and computational methods. Physics, chemistry, biology and statistics are also important.
• You need to be passionate about using mathematics to solve practical problems from other disciplines.
• You will also need to acquire statistical techniques and approaches associated with data analytics, parameter estimation and fitting of models to data.
Explore careers in applied mathematics
• It is important to participate in study groups in mathematical sciences. Check out the Isaac Newton Institute in Cambridge and the International Centre for Mathematical Sciences in Edinburgh.
• Dr Darren Baskill, in the School of Mathematical and Physical Sciences at the University of Sussex, has developed an outreach programme with Brighton Science Festivals.
• For more information on applied mathematics, careers advice, job opportunities and internship opportunities, visit the Society for Industrial and Applied Mathematics and the Institute of Mathematics and its Applications or the American Mathematical Association.
Meet Anotida
What was your childhood like?
I enjoyed cattle grazing, hiking, playing football, volleyball and basketball, as well as reading and playing chess. Growing up, I learnt that hard work pays! Whilst harvesting was a great joy, it was planting seeds that was the essential work. You must plant the seeds of knowledge by developing new areas of study; you only reap what you sow.
I was motivated to study hard when I was young. I lived in poverty and had to work in building construction on weekends and term holidays to afford my boarding school fees at Pakame High School in Shurugwi, Zimbabwe. I realised early on that mathematics was akin to my second name. I was the only student to obtain an A in ordinary level mathematics out of a cohort of approximately 150 students. It was then that I realised that I had the potential to do well in mathematics.
What has your research looked at?
Alongside my PhD, I have a bachelor’s degree in applied mathematics and a master’s degree in mathematics and education. I joined a group in mathematical biology at the University of Oxford, where my numerical analysis and modelling techniques fitted naturally with the research questions being addressed at the time.
Amongst several other projects, I have looked at how patterns form in nature, based on Turing’s idea of pattern formation driven by diffusion. I have used mathematical models to look at how cells migrate through complex environments. I have also worked in high performance scientific computing, an area which is key to delivering useful models that can be used by experimentalists and other users in modelling and numerical analysis.
What are you passionate about?
Working with non-mathematicians, such as experimentalists or public health analysts, to formulate new mathematics based on physical observations and principles. I am also extremely passionate about training a new generation of early career scientists with expertise at the boundary between disciplines: theoretical and experimental.
What other opportunities has your career provided?
I have been lucky enough to have travelled around the world, to all continents. The highlights include my five-year stay in Cuba during the Zimbabwe-Cuba International Higher education collaboration and a three-year stay in Alabama, in the US, that was critical in showing me the need to belong to an appropriate department with expertise complimentary to mine.
Attending international conferences has seen me travel to Penang Island in Malaysia, where I was stung by a jelly fish (we do not have such creatures in Zimbabwe!). I also visited the Amazon as part of my research trip to Brazil to study stingrays. My other favourite places are the Tennessee mountain belt, skiing resorts off Grenoble in France, beautiful churches in Lecce, Italy, and villages outside Shanghai, in China. I should not forget my trip to Hyderabad in India where seeing the mixture of city and wildlife is spectacular; animals can be roaming wildly in the city, tricycles are raving from all angles and buses, cars and humans intermingle continuously with no accidents at all! It is such a complex dynamical system to model!
What are you most proud of?
Being awarded the Royal Society Research Merit Award, the book prize for being the top student in mathematics at the University of Zimbabwe, and the golden medal for being the top student across all subjects from the Zimbabwe-Cuba programme. I would be thrilled if I can be nominated to be a Fellow of the African Academy of Sciences, as well as being a Fellow of the Royal Society. My ambition for the future is to develop new areas of research that will occupy mathematicians for centuries to come.
Anotida’s top tips
1. You are capable of being the best in your area if you work very hard and are humble in your quest for knowledge.
2. Be resilient, resourceful and adaptive.
3. Don’t follow the common hypothesis; you must follow your instincts and strengths, take risks when appropriate. What I have learnt is that every door is there to be opened!
4. When choosing a mentor, choose wisely! I have been lucky to be supervised by two extremely top-drawer advisors: Professors Andrew J. Wathen and Philip K. Maini. I also have been lucky to have been taught by two other brilliant professors at the University of Zimbabwe: Dr David Henwood and Professor Mark Roberts. To my Cuban professors (too many to mention), it was a great pleasure to be under their stewardship.
5. To those from minority backgrounds, the reality is: researchers from minority and under-represented groups always work twice as much as other researchers. This is a simple fact of reality.
Do you have a question for Anotida?
Write it in the comments box below and Anotida will get back to you. (Remember, researchers are very busy people, so you may have to wait a few days.)











Hello sir, am passionate in mathematics especially in applied mathematics as am doing undergraduate degree in my final year. What are some of project in applied mathematics?
Hi Benjamin,
I am delighted that you are passionate about mathematics. That is a great start!
Now, there are many areas of research in applied mathematics. From my research program, I work on various projects emerging from cellular and developmental biology where mathematics plays a pivotal role in understanding mechanisms for single and collective cell migration and the formation of pattern formation in nature. Typical projects involve data-driven mathematical modelling involving both continuum mechanics and semi-linear parabolic partial differential equations (of which ordinary differential equations are a subset of); rigorous mathematical analysis of such problems (e.g. existence, uniqueness of solutions, linear or weakly nonlinear analysis in the context of asymptotic analysis); development of novel numerical methods to solve the models both in space and time (in some cases, when the space itself is part of the solution being sought), their rigorous numerical analysis (existence, uniqueness, positivity, boundedness of strong or weak solutions depending on the numerical method developed), applications of the models to experimental observations and finally, to close the loop, using data to constrain the models through model selection and parameter inference (here one needs to develop optimal control or Bayesian methods to fit models to data and to carry out parameter estimation). Within this cyclic research approach, one can find many projects to study, either from a theoretical, analytical, numerical, computational and statistical point of view. The choice really depends on one’s mathematical strengths and expertise as well as the passion to learn new methodologies and techniques. Applications of such models are prevalent in cancer biology, wound healing, burns, inflammation, and many others.
Other areas of research in applied mathematics include epidemiology, infectious diseases, material and biomedical sciences, population dynamics, game theory, economics, climate modelling, fluid dynamics, etc.
I am super happy to chat to you more specifically about applied mathematics in my research area. I hope you find this reply useful, if not, get in touch, happy to provide further clarity to the reply.
I am a Zimbabwean academic but working in South Africa, full professor of Mathematics Education and a member of the World Council for Gifted & Talented Children (WCGTC). I am interested in research on the mathematically gifted children – any chance of doing collaborative work.