Like sport but hate maths? Think again!
This blog post was written by Isla Simmons of Futurum Careers
Have you ever considered how maths plays a role in sports? There are obvious examples such as counting goals in football, or subtracting scores in darts, but all sports have elements of maths within them.
Measuring your heart rate when you exercise will tell you how you are training your body – you are exercising aerobically if your heart rate is 50-70% of its maximum (calculated as 220 minus your age). Aerodynamic equations are used when designing cycling helmets or racing cars, reducing the drag and so increasing the speed. And when you hit a ball in pool, you’ll need some equations from mechanics to determine the speed and direction that it bounces off the edge of the table.
One great example of a sport full of maths is orienteering, which combines running with navigation. Competitors are given a map (of a forest, mountainside, park or city centre) with a course marked on it, and the aim is to navigate around the course in the quickest time possible. This means that the best orienteers are not necessarily the fastest runners, but those who can also find their way.
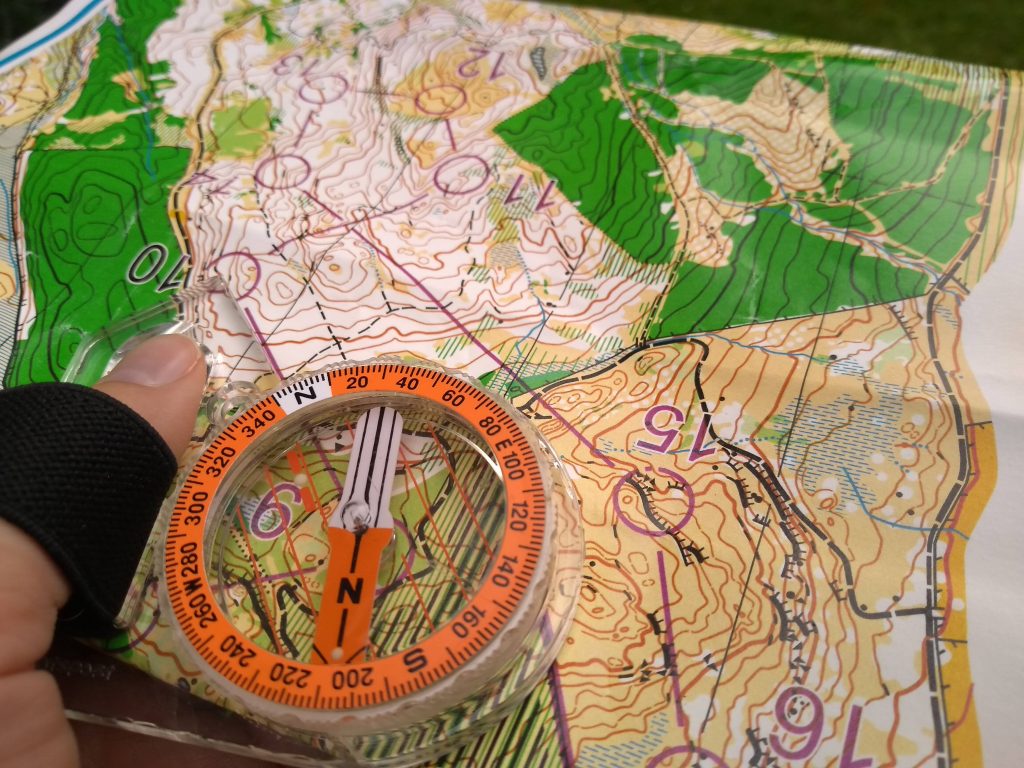
I love orienteering because it combines the physical challenge of running with the mental challenge of navigation. To determine how to get from Point 1 to Point 2, I first need to read and understand the map and relate this to the terrain around me. Is the ground flat or inclined? What features are nearby – cliffs, fences, streams, boulders?
Route choice is a key part of navigation – working out which way to go. Should I take a compass bearing and run in a straight line through the forest (requiring a certain amount of skill to ensure that I don’t veer off in the wrong direction)? Or should I take a longer but safer route following paths that will guide me to my destination?
As well as the mathematical skills involved in compass bearings, there are also the issues of scale and distance. Most orienteering maps are at a scale of 1:10,000 meaning that 1 cm on the map equals 100 m (10,000 cm) on the ground. But some are at 1:15,000 or 1:7500, meaning 1 cm on the map equals 150 m or 75 m on the ground, respectively. So, if my destination is 3 cm away on the map, the map scale determines whether I need to run 300 m, 450 m or 225 m.
And once I know how far I have to run, I then need to judge my distance as I’m running. I take approximately 47 double paces to run 100 m along a path, so to run 300 m requires about 141 paces. But my steps will be shorter when running uphill or through undergrowth, so I’ll also need to factor in some extra paces to account for this. All of which means I have plenty to occupy my brain with as I complete a course!
“What I love about orienteering is the fact that there is more to it than other sports,” says 17-year-old Rachel, who won her class at the Scottish Orienteering Championships last weekend. “I love the element of problem solving and the challenge of the sport, as well as the amazing forests and hillsides that you’d otherwise never see.” Not only is Rachel Scottish Champion, but she has also been selected to run in the Junior World Orienteering Championships, which will be held in Turkey in September, after which she’ll be heading to the University of Edinburgh to study Maths and Statistics.
If you want a challenge for both body and mind, perhaps orienteering is the sport for you!
Find out if there are any orienteering events happening near you: www.britishorienteering.org.uk/newcomers_guide
Rachel and I are both members of Edinburgh Southern Orienteering Club: www.esoc.org.uk
