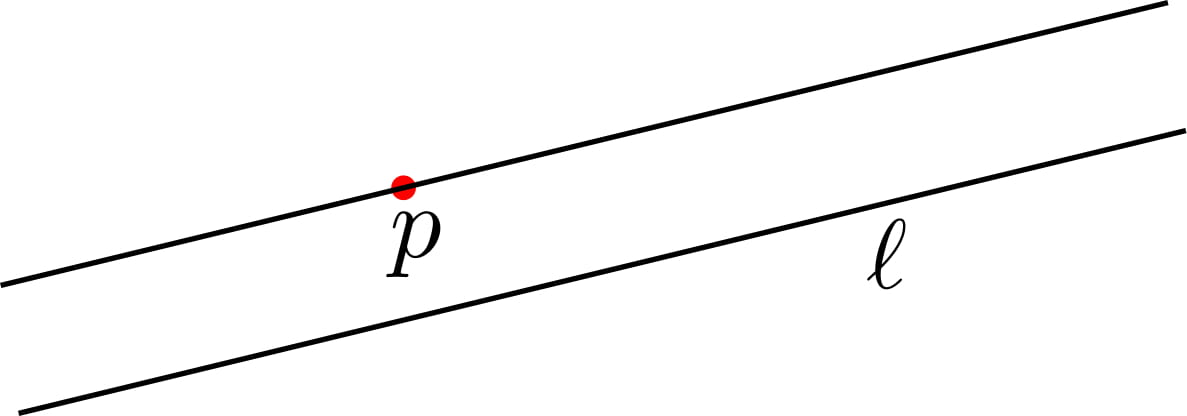Mathematics: plane and simple
Dr Sam Ballas is based at Florida State University in the US. His research focus is on geometry and surfaces, which is a branch of mathematics. Sam’s passion for the subject shows that although maths can be challenging, it can also be extremely rewarding
TALK LIKE A MATHEMATICIAN
TOPOLOGY
The study of geometrical properties and spatial relations that are unaffected by changes to the shape or size of figures. To a topologist, a coffee cup and a doughnut are the same shape, since one can be deformed to the other without tearing!
CONVEX
A shape is convex if any two points can be connected by a straight line that is contained in the shape.
PROJECTIVE GEOMETRY
A topic in mathematics that studies geometric properties that are invariant with respect to projective transformations. An example is a film projector projecting a movie onto a screen. This is also how our vision works, where objects at different distances are projected onto our ‘visual sphere’. This is why when you look down a set of railway tracks, they look like they start to get close together.
MANIFOLD
A topological space that ‘locally’ resembles Euclidean space. A manifold is a higher dimensional analogue of a surface in two dimensions or a circle in one dimension.
PLANE
A flat, two-dimensional surface that extends infinitely far.
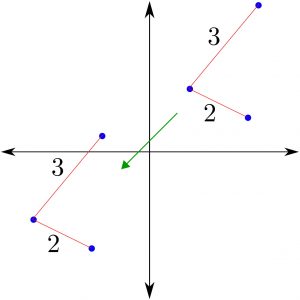
TRANSLATION
A geometric transformation that moves every point of a figure or a space by the same distance in a given direction.
Before > After
ROTATION
A motion of a certain space that preserves at least one point.
Before > After
GENUS
A topologically invariant property of a surface defined as the largest number of non-intersecting simple closed curves that can be drawn on the surface without separating it. Intuitively, this is the number of holes in a surface.
TORUS
A two-dimensional shape made by revolving a small circle along a line made by a bigger circle – it often looks like a doughnut or rubber ring. We usually view it in three-dimensional space, but it is really just the ‘skin’ of the doughnut, which has no thickness.
Geometry is a branch of mathematics that is concerned with the size, shape, positions, angles and dimensions of things. We are all familiar with geometric shapes in two dimensions, such as a square, circle, triangle and rectangle, and three dimensions, such as a cube, triangular prism, square-based pyramid and cuboid. However, while those examples are clear and easy to follow, there are mathematicians that are engaged with geometrical problems so complex that explaining them in ways that are easy to understand is extremely difficult. For example, though we view a sphere in a three-dimensional space, it is like a torus and is actually a two-dimensional shape! Indeed, understanding many geometric problems is much easier if you can visualise what is being described rather than merely reading words.
Dr Sam Ballas, who is based at Florida State University in the US, is a mathematician who is focused on geometry of surfaces and their higher dimensional cousins, manifolds. “My interest in geometry stems from my always trying to understand things visually and I am always trying to draw pictures of things to help me better understand them,” says Sam. “I also like to think about how different objects can be stretched and deformed to one another. For me, this type of approach has always been helpful in studying geometric problems.”
WHAT ARE THE MAIN TOPICS OF SAM’S RESEARCH?
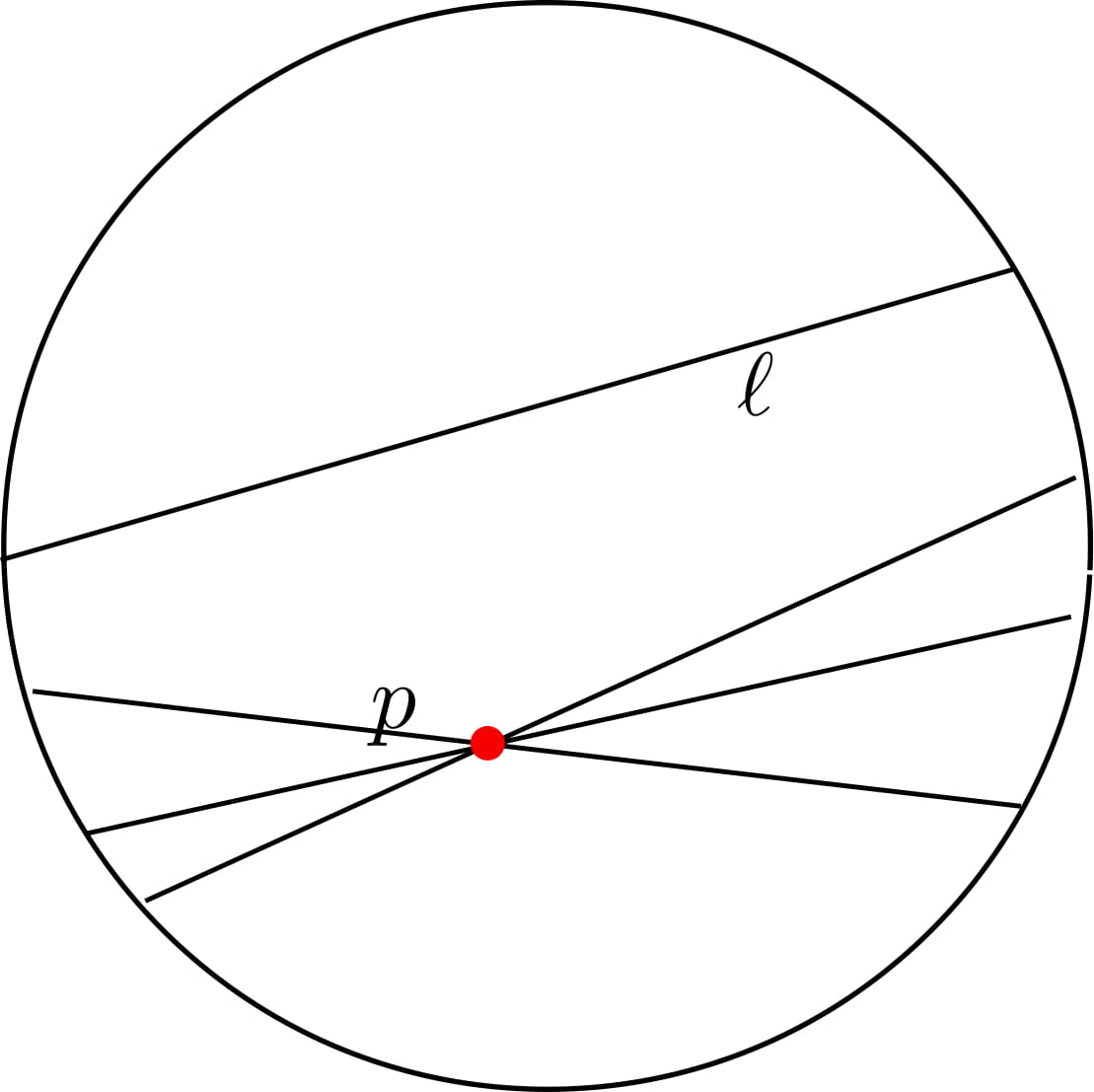
Sam is involved in several related projects, but one of his main topics of enquiry is the geometry and topology of convex projective manifolds. His work focuses on something known as the hyperbolic plane, which can be thought of as the exotic cousin of the standard plane, and both share many properties. “Both of these planes have a notion of straight lines and angles, and you can do a lot of things in the hyperbolic plane that you can do in the regular plane, such as connect any two points with a straight line,” explains Sam. “The main difference is that there are a lot more parallel lines in the hyperbolic plane.”
Reference
https://doi.org/10.33424/FUTURUM85
TALK LIKE A MATHEMATICIAN
TOPOLOGY
The study of geometrical properties and spatial relations that are unaffected by changes to the shape or size of figures. To a topologist, a coffee cup and a doughnut are the same shape, since one can be deformed to the other without tearing!
CONVEX
A shape is convex if any two points can be connected by a straight line that is contained in the shape.
PROJECTIVE GEOMETRY
A topic in mathematics that studies geometric properties that are invariant with respect to projective transformations. An example is a film projector projecting a movie onto a screen. This is also how our vision works, where objects at different distances are projected onto our ‘visual sphere’. This is why when you look down a set of railway tracks, they look like they start to get close together.
MANIFOLD
A topological space that ‘locally’ resembles Euclidean space. A manifold is a higher dimensional analogue of a surface in two dimensions or a circle in one dimension.
PLANE
A flat, two-dimensional surface that extends infinitely far.
TRANSLATION
A geometric transformation that moves every point of a figure or a space by the same distance in a given direction.
Before > After

ROTATION
A motion of a certain space that preserves at least one point.
Before > After

GENUS
A topologically invariant property of a surface defined as the largest number of nonintersecting simple closed curves that can be drawn on the surface without separating it. Intuitively, this is the number of holes in a surface.
TORUS
A two-dimensional shape made by revolving a small circle along a line made by a bigger circle – it often looks like a doughnut or rubber ring. We usually view it in three-dimensional space, but it is really just the ‘skin’ of the doughnut, which has no thickness.
Geometry is a branch of mathematics that is concerned with the size, shape, positions, angles and dimensions of things. We are all familiar with geometric shapes in two dimensions, such as a square, circle, triangle and rectangle, and three dimensions, such as a cube, triangular prism, square-based pyramid and cuboid. However, while those examples are clear and easy to follow, there are mathematicians that are engaged with geometrical problems so complex that explaining them in ways that are easy to understand is extremely difficult. For example, though we view a sphere in a three-dimensional space, it is like a torus and is actually a two-dimensional shape! Indeed, understanding many geometric problems is much easier if you can visualise what is being described rather than merely reading words.
Dr Sam Ballas, who is based at Florida State University in the US, is a mathematician who is focused on geometry of surfaces and their higher dimensional cousins, manifolds. “My interest in geometry stems from my always trying to understand things visually and I am always trying to draw pictures of things to help me better understand them,” says Sam. “I also like to think about how different objects can be stretched and deformed to one another. For me, this type of approach has always been helpful in studying geometric problems.”
WHAT ARE THE MAIN TOPICS OF SAM’S RESEARCH?
Sam is involved in several related projects, but one of his main topics of enquiry is the geometry and topology of convex projective manifolds. His work focuses on something known as the hyperbolic plane, which can be thought of as the exotic cousin of the standard plane, and both share many properties. “Both of these planes have a notion of straight lines and angles, and you can do a lot of things in the hyperbolic plane that you can do in the regular plane, such as connect any two points with a straight line,” explains Sam. “The main difference is that there are a lot more parallel lines in the hyperbolic plane.”
In the regular plane, if you have a line and pick a point not on that line, there is only one line parallel to your line through that point. However, on the hyperbolic plane, there are infinitely many more lines through your point and parallel to your line. Knowing this has many important consequences, such as the fact that many nearby straight lines ‘spread out’ very quickly – this makes them useful for modelling chaotic behaviour, where small changes in initial conditions cause large changes in overall behaviour.
WHAT ARE THE MAIN HIGHLIGHTS OF SAM’S WORK?
One of Sam’s favourite results so far is showing that certain three-dimensional objects can be glued together to form more interesting objects. “The thing I liked most about this result is that it generalised a nice and well-known two-dimensional picture of gluing together surfaces, but was previously unknown in the third dimension,” says Sam. “This analogy was very helpful for me and my collaborators when we were trying to prove the result because we could fall back to the more familiar two-dimensional setting for inspiration.”
DOES SAM’S WORK HAVE ANY ‘REAL LIFE’ APPLICATIONS?
Yes! One of the applications of Sam’s work is that certain geometric objects can be used to produce what are called expander graphs. Informally, a graph is just a collection of dots (called vertices) where some of the dots are connected to each other by lines (called edges). You can think of graphs as physical objects, but you can also think of them as network connections between two computers,” says Sam. “Roughly speaking, an expander graph is one that has many more vertices than edges but is still very hard to disconnect by removing a small number of edges.”
Such a graph could be useful for building a robust computer network, as it would require relatively few connections, but the link between two computers cannot be broken without many connections being severed.
 DR SAM BALLAS
DR SAM BALLAS
Department of Mathematics, Florida State University, USA
FIELD OF RESEARCH: Mathematics
RESEARCH PROJECT: Sam’s research is concerned with a wide range of mathematical problems. One of his main interests in the hyperbolic plane, which can be particularly useful for modelling chaotic behaviour, where small changes in initial conditions can cause large changes in overall behaviour.
FUNDER: National Science Foundation
ABOUT MATHEMATICS
The history of mathematics is long and varied. From the notched bones in prehistoric Africa (which provide evidence of our thinking about numbers), the Moscow Papyrus (the oldest mathematical text from ancient Egypt), through to Isaac Newton’s use of calculus in the laws of motion and gravitation, maths has provided mankind with a means of understanding the world (and universe)
around us.
One of the main attractions of maths is that its work is never done; every century since the Renaissance has seen more mathematical problems solved than the century before, yet many problems remain unsolved. In 2000, the Clay Mathematics Institute posited seven Millennium Prize Problems which were thought to be some of the most difficult problems mathematicians were grappling with. Since then, only one – the Poincaré Conjecture – has been solved, with Dr Grigoriy Perelman claiming the honours and being awarded $1 million (which he rejected on account of his believing his contribution to the solution was no greater than that of Richard S.
Hamilton’s).
Perhaps you could be the one to solve one of the remaining six problems and cement your name in history…
WHAT ARE SOME OF THE KEY QUESTIONS THAT TODAY’S MATHEMATICIANS ARE TRYING TO
ANSWER?
When we spoke to Sam about his work and the broader scope of enquiry within the field of mathematics, he actually referenced a couple of the aforementioned Millennium Prize Problems.
“One of the most interesting problems is the Riemann Hypothesis, which is concerned with the distribution of the prime numbers amongst the integers,” says Sam. “Then there is the P vs NP Problem, which is about quantifying how much harder solving a problem can be than checking that a proposed solution is correct.” One of the clearest examples of this is to think about Sudoku problems – how much harder is it to solve a Sudoku puzzle than verify that one has been completed correctly? Only maths can provide an answer, yet the problem remains unsolved.
ARE THERE ANY OPPORTUNITIES TO COLLABORATE WITH OTHER MATHEMATICIANS?
Mathematicians have collaborated multiple times over the centuries. The old adage, two heads are better than one, certainly applies in the field of maths, although it can often be a solitary pursuit and many mathematicians work on their own volition. Still, Sam is positive about the collaborative environment within maths. “Most of the time, mathematicians are people who are good at taking a problem, stripping away the unimportant extraneous details and revealing the real essence of the problem,” says Sam. “This often makes them able to help make progress on problems where they initially do not have a ton of domain specific knowledge. For instance, I know several mathematicians at Florida State (and elsewhere) who have helped solve important problems in biology, geology, and pharmaceuticals.”
WHAT MAKES A GOOD MATHEMATICIAN?
Sam believes that two attributes in particular make a good mathematician – curiosity and resilience. “For curiosity, I really mean the mindset of always looking for ways in which different things are connected and similar to one another,” explains Sam. “As for resilience, one of the most consistent features of doing almost any kind of research is failure. Most of the things you try are not going to work and it is important to be able to keep going and not be overly discouraged by repeated failure. I would say in my work that I am failing about 90% of the time, but I find the 10% of time I am successful is so rewarding that it helps me push through the other 90%.”
HOW TO BECOME A MATHEMATICIAN
• The Math Learning Center has a host of resources for all levels of ability. Their resources include free math apps covering a wide range of topics, including a Geoboard.
• The Millennium Mathematics Project is a maths education and outreach initiative for ages 3 to 19. It aims to enrich everyone’s experience of mathematics and increase their understanding, confidence and enjoyment.
• The average salary for a mathematician in the United States is $101,900. Wages typically start from $57,150 and go up to $160,550. (https://www.careerexplorer.com/careers/mathematician/salary/)
PATHWAY FROM SCHOOL TO MATHEMATICIAN
Sam believes that two classes that are helpful to pretty much any mathematician are calculus
and linear algebra. These subjects are particularly useful if you are interested in learning about
machine learning and data science, although the benefits of calculus and linear algebra are generally far-reaching.
2 or 3 A levels, or equivalent, including maths
A degree in mathematics, physics or applied mathematics
https://www.careerexplorer.com/careers/mathematician/education/
SAM’S TOP TIPS
1 I really cannot overstate how important I think it is to find something you are interested in and passionate about – that will make it so much easier to overcome any obstacles you might face in your studies because you will really care about what you are doing.
2 It is easy to say from a vantage point of being older, but I highly recommend that when you are young, you should try to learn about as many different things as possible. You never know where your passion might lie and by widening your field of enquiry, you will increase your chances of finding what is right for you.
3 Becoming a mathematician often involves a lot of computing, so I recommend trying to learn to programme in at least one programming language, such as Python. In the current world, programming is an indispensable skill for pretty much any STEM-based career.
THE FIELDS MEDAL
The most prestigious of mathematics prizes, the Fields Medal is awarded to two to four mathematicians every four years at the International Congress of the International Mathematical Union (IMU). WINNERS INCLUDE:
• Grigory Perelman was offered but, again, declined the medal.
• William Thurston is described as ‘pioneer’ in the field of low-dimensional topology. Awarded the medal for his work on manifolds, Thurston has been very influential on Sam’s work.1
• Maryam Mirzakhani, one of the most famous researchers in Sam’s field, was the first woman to win the Fields Medal, awarded to her for her work on “the dynamics and geometry of Riemann surfaces and their moduli spaces”. Unfortunately, she died recently and at only 40 years old, but her story is inspirational and worthy of further reading.2
1https://en.wikipedia.org/wiki/William_Thurston
2https://en.wikipedia.org/wiki/Maryam_Mirzakhani
HOW DID DR SAM BALLAS BECOME A MATHEMATICIAN?
WHAT WERE YOUR INTERESTS AS A CHILD? DID YOU ALWAYS KNOW YOU WANTED TO BE A MATHEMATICIAN?
Being a mathematician was definitely not on my radar when I was a kid! My father is a physician and growing up, I always envisioned myself going into medicine. I didn’t really get into maths until I was at university and had the opportunity to take more interesting and advanced maths classes. This was the first time I got to see that maths was a lot more than the rote computations and formulas that I had been previously exposed to.
WHO HAS INSPIRED YOU IN YOUR CAREER?
I have had the pleasure of being able to learn from and be mentored by a lot of amazing people throughout my career. If I listed everyone who has inspired me, it would be an extremely long list, but a few who stand out are Emily Hamilton, Frank Pajares, Alan Reid, Ted Odell, Daryl Cooper and Darren Long.
HOW DO YOU OVERCOME OBSTACLES IN YOUR WORK?
I think resilience is key to overcoming challenges in my work. It is important to develop a feel for when you are making progress but haven’t quite made it to the end, and when you are truly stuck. Of course, this is easier said than done and is often only obvious in retrospect. It is also good to have a few different things to work on at any given time – that way you can turn your attention to something else if you are stuck on a project. There have definitely been times where I have felt stuck, gone to work on something else, and then come back to my original problem with fresh eyes and was able to make progress.
HOW DO YOU ‘SWITCH OFF’ FROM YOUR ACADEMIC WORK?
This can be a real challenge at times. When I have a problem I am really interested in it’s usually the last thing I think about at night and the first thing I think of when I wake up (sometimes even in the middle of the night!). Something that has helped in recent years is becoming a dad. Being a parent requires a lot of your focus and when my son, Eli, wants to play with me, he is not typically very sympathetic if I tell him that “Dada is thinking about a math problem right now!” If you don’t think that having a child for the purpose of switching off from your academic work is a good strategy for you, then you can also try exercising – I have also had some success with that!
HAVE YOU SET YOURSELF ANY GOALS YOU WOULD LIKE TO REACH IN THE FUTURE?
In a broad sense, I would like to continue to study and make progress on problems that I find interesting. I would also like to become more involved in graduate education and outreach activities – to this end, one of my more tangible goals is to establish an experimental mathematics lab at Florida State where students can work in small groups on projects that focus on math as an experimental science. The idea is that students will form hypotheses and design and implement experiments to test them.
Do you have a question for Sam?
If you are intrigued by the challenge Sam has set on his activity sheet, send him a message – he’ll help you!