Predicting the future: the power of modelling

ALLELE – two or more forms of a gene that determine certain observable traits, such as resistance or vulnerability to an insecticide, or hair colour

CHROMOSOME – a part of human, animal and plant cells that carries hereditary information in the form of genes

COEFFICIENT – a value describing the relative importance/weight of parameters in a model

ECOLOGY – the study of relationships among organisms and their physical environment

EMIGRATION – the act of individuals leaving a particular population

ENTOMOLOGY – the study of insects

FITNESS COST – the ‘cost’ of developing resistance. For example, resistant individuals may have fewer offspring or live shorter lives, meaning that non-resistant individuals may have a competitive advantage over resistant individuals when the given insecticide is not being used

GENE – a location on a chromosome that is inherited from parents. Each gene can have two or more forms, which are referred to as alleles

GENOTYPE – an arrangement of genes that determine an organism’s hereditary potentials and limitations

IMMIGRATION – the act of individuals joining a particular population

INSECTICIDE – a substance that kills insects

MODEL – in science, a mathematical representation of how one or more parameters cause a change in criteria

MORTALITY RATE – the proportion of dead individuals in a population (opposite of survival rate)

PARAMETER – a measurable element of a model

POPULATION DYNAMICS – the study of changes in populations over time or space

QUANTIFIABLE – something that can be measured

REPRODUCTIVE RATE – how many offspring each female produces in each generation

RESISTANCE – the ability of an organism to resist (not die of) a particular threat

RESISTANCE ALLELE FREQUENCY – the frequency of the allele that creates genetic resistance against a given insecticide

SURVIVAL RATE – the proportion of live individuals in a population (opposite of mortality rate)

UNIVOLTINE – refers to organisms that can have only one set of offspring per year

VARIABLE – an element that changes and affects a particular output

Dr Christian Nansen is a professor in the Department of Entomology and Nematology at the University of California, Davis. His teaching, mentoring and research focus on capacity building and innovative solutions within the areas of sustainable food production and pest management. In previous research, Christian worked with drones, robotics, machine vision, phone apps and other technologies. Recently, he developed a freely available model to study insecticide resistance evolution and predict outcomes based on readily available information.

Consider baseball, or any other competitive sport, and imagine predicting a team winning lots of matches and possibly a championship at the end of the season. That is a very complex challenge, which involves considering the performance of all the different team players, the defensive and offensive strategies during a long game (nine innings) and the qualities of other competing teams.

You may think that no one could predict who will win. “True, no one can make a 100% reliable prediction, but it turns out that the game of baseball can be ‘broken down’ into a complex sequence or network of individual events, and each of them can be described mathematically,” explains Christian.

“There is a very popular movie (based on true events), Moneyball, describing how a general baseball team manager hired a modelling genius, who developed a mathematical model and was able to predict which players to pick for the team and how they should be playing for the Oakland Athletics to maximise their likelihood of winning matches,” he says. “I strongly recommend you watch this movie and, while watching it, think about how and why it is much more than a movie about baseball.”

In this article, a freely available model about insecticide resistance evolution is used as a case study. But, just like Moneyball is a movie about much more than ‘just’ how to win baseball matches, the model describing insecticide resistance evolution is used to discuss something of much broader relevance. The goal is to demonstrate the purpose and importance of modelling in the classroom. As a basic framework, modelling can be taught to empower and inspire future generations of scientists, teachers and decision-makers.

MODELLING IN DAILY LIFE

Although we may not realise it, we are making model predictions every time we make a decision and/or take an action. “For instance, when we go cycling, we choose to cycle on the road,” says Christian. “Our experience tells us that it is better to ride on a road rather than try to cycle through a house.”

Our experiences also give us a set of ‘rules’ that we follow so that we act appropriately in different situations. Cycling on the streets in the UK and the US has one major difference, which becomes evident very quickly. In the UK, traffic is on the left side, while it is on the right side in the US. So, different models are used to maximise our safety while cycling in different countries, and mathematical models work in the same way.

“Models are adapted to local conditions and that leads to specific outcomes. The more information we put into the model, the more likely it is that the model represents our current body of knowledge about the particular challenge,” Christian explains. “If a model is detailed, that is, it includes many parameters, it is also more likely to produce meaningful and useful predictions.”

When making predictions about complex issues, it is important to remember that models are never 100% accurate – they are associated with some degree of ‘error’ (inaccuracy). “Take your health as an example,” says Christian. “We know from experience and education that exercise is good for our health, and smoking and alcohol are bad for our health, so we can ‘predict’ that adopting a habit of smoking, for instance, will affect our health negatively.”

From decades of scientific study, we know that smoking is likely to have a more significant impact on our health than some other unhealthy habits, such as drinking coffee or sugary soft drinks. But it is not 100% certain that smokers get ill or die younger than non-smokers, because many variables determine our health.

For example, coffee or sugary soft drinks may be particularly harmful to certain people with other health conditions. “But we can make general recommendations based on what we know and based on what is most likely to happen,” says Christian. “And then we can develop specific models for children, men, women or other specific demographic groups – this is precisely how fitness watches model our health and give us suggestions of how to stay healthy.”

MODELLING OF INSECTICIDE RESISTANCE EVOLUTION

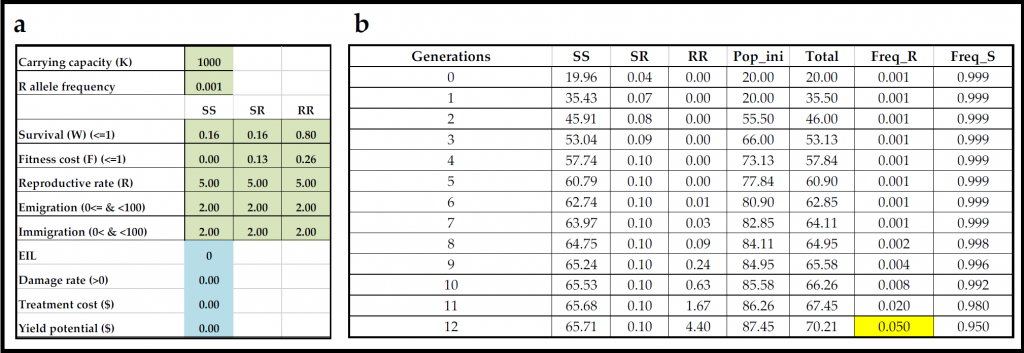
“The science behind this model involves a general understanding of genetics, evolutionary processes, insect population dynamics and economics of crop production and pest management,” explains Christian. This means that a wide range of different variables, biological and economical, are known to interact in complex ways and influence the likelihood of a particular insect pest population developing resistance to an insecticide over generations of insect pests.

“Many people understand the concerns and risks associated with resistance to antibiotics; certain medications are no longer capable of protecting us against bacterial infections because the bacteria have developed resistance,” says Christian. “The same challenge is evolving in agriculture; insect pests that cause damage to livestock or crop production systems evolve resistance to the insecticides used to control them.” This gene is assumed to have two alleles, which are two forms of the gene – these forms are ‘R’ (resistant) or ‘S’ (susceptible).

Because almost all insects are diploid (have two complete sets of chromosomes), it means that for this gene, all insects have one of these three genotypes: SS, SR or RR. Although genotypes can interbreed, they are assumed to have different growth parameters (for instance, how long they live, how many eggs they lay or survival rates of different life stages). Another critically important aspect of predicting resistance evolution is to obtain information about allele frequencies: how rare is the resistance allele?

“When an insecticide is applied to a crop, it acts as a selection pressure on the pest population – it will kill individuals that are susceptible but not the individuals that (based on their unique behaviour or genetic make-up) are resistant,” explains Christian. If one in five (20%) of pest individuals is resistant, then, in a few generations, the total population will be completely resistant, because that is a very high level of resistance. In most studied cases, resistance allele frequencies are 1 in 1,000 (0.001 – 99.9% are susceptible), so it takes 10 or more generations before resistance alleles become abundant within insect populations. But it is not only resistance allele frequency that determines how quickly resistance develops.

When you buy disinfectants to clean surfaces in bathrooms or kitchens, you will often see on the label that these products are assumed to kill 99.99% of germs, bacteria or pathogens (whatever term they use to describe ‘the bad guys’) so only 1 in 10,000 survives. This sounds excellent, but if there are 1 million bad bacteria on a kitchen surface (which is possible), 100 bacteria (0.0001 × 1,000,000) will survive the cleaning process!

The first time the cleaning agent is used, the bacterial population will be significantly reduced, but it may be able to gradually rebound if the resistant individuals are allowed to thrive and multiply, and if they have a high growth rate. Christian explains that if they do, then there has likely been a shift in the population’s genetic composition: before cleaning, the vast majority were SS, while after several generations and selection pressure by the cleaning agent, the bacterial population becomes predominantly highly resistant, RR.

“Therefore, when antibiotics are 1) prescribed too frequently to patients and 2) given excessively to livestock to stimulate growth and protect against infections, antibiotic resistance becomes a problem,” says Christian. “Similarly, if bacterial cleaning products are used widely and excessively, then they may lose their effect over time for the same reason.”

A REAL-WORLD CHALLENGE

There is a fundamental dilemma in health care and pest management in agriculture: we want to use the most effective medicine, cleaning agents and pesticides. But the most effective products should only be used as a last resort, because if used too widely and frequently, human diseases, surface pathogens or crop pests may develop resistance.

Because of this basic dilemma, modelling can be used to optimise the use of an insecticide to achieve the highest level of pest control over time and, at the same time, minimise the risk of pest populations developing resistance. That is the basic biological challenge, and then we can add an economical dimension to optimise the economic sustainability of pest management.

“By now, I hope you can appreciate that, although modelling effects of climate change and minimising risks of insecticide resistance evolution are different from modelling outcomes of baseball games – there are striking similarities!” says Christian. “We have great interest in predicting outcomes, these challenges are highly complex, and each can be broken down into a series of parameters in a model.”

Christian explains that in the model of insecticide resistance evolution, decades of research have provided ample insight into critical variables; these include reproductive rate, immigration rate, emigration rate, resistant allele frequency and fitness cost. These and other variables have been included as parameters in the model, and they can be examined in different combinations. The model is freely available as an interactive Excel spreadsheet. “Through hands-on experience with this and similar interactive teaching tools, students will acquire fundamental knowledge about basic population models and gain experience with quantitative data interpretation,” Christian explains. The model can be downloaded freely from Christian’s website (chrnansen.wixsite.com/nansen2/teachingtool), which also offers a tutorial video on using the model.

MODELLING AND TEACHING

Christian believes that teachers and students will benefit from the interactive teaching tool. “Teachers can use the interactive tool to demonstrate how models can help visualise complex interactions,” says Christian. “Students can use the tool to test different scenarios and observe the effects of changing parameters.”

Rather than a learning process focused on memorisation, the teaching tool encourages students to think about why various scenarios lead to different outcomes, and how these outcomes can be influenced. Many young people express deep anxieties about the future of the world and, often, with good reason.

Christian believes that models can help address these worries. “Models help show that the future is somewhat ‘predictable’ – which means that certain outcomes can be avoided,” says Christian. “This shows students that, provided we adjust the underlying variables, we have the power to change the future.”

DR CHRISTIAN NANSEN
Professor of Entomology and Nematology, College of Agriculture and Environment, University of California, Davis, USA

FIELD OF RESEARCH: Insect Ecology and Management

RESEARCH PROJECT: Developing an interactive teaching tool that describes resistance evolution and basic economics of insecticide-based pest management

DR CHRISTIAN NANSEN
Professor of Entomology and Nematology, College of Agriculture and Environment, University of California, Davis, USA

FIELD OF RESEARCH: Insect Ecology and Management

RESEARCH PROJECT: Developing an interactive teaching tool that describes resistance evolution and basic economics of insecticide-based pest management

Do you have a question for Christian?
Write it in the comments box below and Christian will get back to you. (Remember, researchers are very busy people, so you may have to wait a few days.)