Solving the Tower of Hanoi
The Tower of Hanoi is a beguiling puzzle that has entranced mathematicians for almost 140 years. Despite its apparent simplicity, it continues to yield new surprises – as mathematics professor Dan Romik can testify. His work has revealed new secrets about the puzzle, and through it, important lessons for the wider world of mathematics
TALK LIKE A MATHEMATICIAN
DISCRETE MATHEMATICS – the study of mathematical structures that are countable and separable, rather than continuous
EXPONENTIAL – IN MATHEMATICS, CONTAINING AN EXPONENT – a number that shows how many times another number is to be multiplied by itself
FRACTAL – a shape for which any part is a larger or smaller version of another part. Watch this BBC Ideas video on YouTube for a detailed explanation: https://www.youtube.com/watch?v=w_MNQBWQ5DI
RECURSION – the repeated application of a procedure that involves breaking down the procedure into smaller, similar parts
TOWER OF HANOI – a mathematical puzzle involving moving a tower of discs from one pole to another, while obeying certain rules
In 1883, a French mathematician named Édouard Lucas came up with an intriguing scenario. There are three poles in a row, the one on the left containing a series of discs of decreasing size, with the other two, empty. The aim is to move the tower, one disc at a time, over to the right-hand pole. However, the catch is, a larger disc can never sit on top of a smaller disc. This puzzle quickly reached fame as the brainteaser now known as the Tower of Hanoi.
Despite it seeming initially perplexing, in truth the Tower of Hanoi is a problem that even amateur puzzlers can solve with a bit of lateral thinking. However, underlying the puzzle are some key mathematical ideas – even if we might not appreciate them when solving it. Professor Dan Romik, of the University of California, Davis, has investigated the Tower of Hanoi and, despite the puzzle’s apparent simplicity, has shown that it continues to yield new surprises.
RECURSION
“Recursion is the extremely useful idea of solving a large problem by reducing it to smaller instances of the same problem,” says Dan. For instance, imagine you have eighty coins and a set of balance scales. All the coins weigh the same, apart from one that weighs slightly less. To find this lighter coin, one solution would be to weigh and compare two coins at a time to see if there is any difference in weight – but this method would take ages. A faster way would be to divide the pile into two piles of forty and weigh these two piles against one another. You can select the lighter pile and discard the other forty coins all at once. You then repeat this process, dividing the pile into two twenties, two tens, and so on, until you narrow it down to the one coin.
The Tower of Hanoi can be solved using recursion too, which helps mathematicians find the way to solve the puzzle in the fewest number of steps possible. Ultimately, it involves constructing and reconstructing progressively larger ‘towers’, until the bottom disc can be moved to the third pole and the rest of the tower constructed upon it, as the text box explains in mathematical terms (See ‘Solving the Tower of Hanoi through recursion’ on the third page). The more discs that the puzzle contains, the more steps it will take – rising exponentially, in fact. This can be written in algebraic form: S = 2N-1
In this formula, S is the number of steps, and N is the number of discs. So, if the tower had five discs, the formula would be 2⁵-1, which is 31. Therefore, solving the puzzle would take a minimum of 31 steps. If it had four discs, it would require only 15 steps – and for three discs, only 7.
Interestingly, this formula can lead us back to the Tower of Hanoi’s supposed mythological roots. The legend goes that young priests of a Hindu temple were tasked with moving discs of pure gold according to the rules of the puzzle – except that their Tower contained not 5 but 64 discs, and it was said that when they completed the task, the world would end. Using the formula above, we can deem that this is highly unlikely, given it would take them many billions of years to complete! Since this legend was invented by Lucas as a marketing ploy, it is hardly surprising that the underlying mathematics do not allow this apocalyptic prophecy to be put to the test.
GRAPHICAL REPRESENTATION
To visualise not only how many steps are needed, but exactly which steps too, the Tower of Hanoi configuration can be represented on a diagram that mathematicians call a graph. Graphs uncover aspects of a particular scenario that might have otherwise gone unseen, in particular by connecting them to other scenarios that may be better understood. “Many problems in discrete mathematics can be translated onto a graph, such as scenarios that involve flipping a switch or making a move in chess,” says Dan. “Once you have represented the problem this way, you can spot connections to other problems you already know about.”
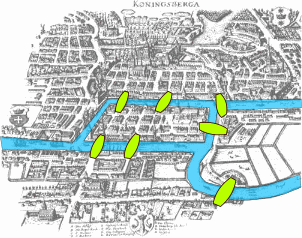
This mode of thinking originated when mathematician Leonhard Euler was tasked with the ‘Seven Bridges of Königsberg’ challenge in 1736. Königsberg was a Prussian city bisected by a river that contained two large islands. The four areas between the islands and the two sides of the city were connected by seven bridges. Euler’s challenge was to find a route through the city that involved crossing all seven of the city’s bridges exactly once. He realised that the simplest way to approach the problem was to represent it as a graph, where lines (the bridges) connected four points (the banks and islands) in a way representative of the city’s actual layout. Once he had done this, he was able to easily demonstrate that the challenge was impossible. See the image on the right.
Reference
https://doi.org/10.33424/FUTURUM145
DISCRETE MATHEMATICS – the study of mathematical structures that are countable and separable, rather than continuous
EXPONENTIAL – IN MATHEMATICS, CONTAINING AN EXPONENT – a number that shows how many times another number is to be multiplied by itself
FRACTAL – a shape for which any part is a larger or smaller version of another part. Watch this BBC Ideas video on YouTube for a detailed explanation: https://www.youtube.com/watch?v=w_MNQBWQ5DI
RECURSION – the repeated application of a procedure that involves breaking down the procedure into smaller, similar parts
TOWER OF HANOI – a mathematical puzzle involving moving a tower of discs from one pole to another, while obeying certain rules
In 1883, a French mathematician named Édouard Lucas came up with an intriguing scenario. There are three poles in a row, the one on the left containing a series of discs of decreasing size, with the other two, empty. The aim is to move the tower, one disc at a time, over to the right-hand pole. However, the catch is, a larger disc can never sit on top of a smaller disc. This puzzle quickly reached fame as the brainteaser now known as the Tower of Hanoi.
Despite it seeming initially perplexing, in truth the Tower of Hanoi is a problem that even amateur puzzlers can solve with a bit of lateral thinking. However, underlying the puzzle are some key mathematical ideas – even if we might not appreciate them when solving it. Professor Dan Romik, of the University of California, Davis, has investigated the Tower of Hanoi and, despite the puzzle’s apparent simplicity, has shown that it continues to yield new surprises.
RECURSION
“Recursion is the extremely useful idea of solving a large problem by reducing it to smaller instances of the same problem,” says Dan. For instance, imagine you have eighty coins and a set of balance scales. All the coins weigh the same, apart from one that weighs slightly less. To find this lighter coin, one solution would be to weigh and compare two coins at a time to see if there is any difference in weight – but this method would take ages. A faster way would be to divide the pile into two piles of forty and weigh these two piles against one another. You can select the lighter pile and discard the other forty coins all at once. You then repeat this process, dividing the pile into two twenties, two tens, and so on, until you narrow it down to the one coin.
The Tower of Hanoi can be solved using recursion too, which helps mathematicians find the way to solve the puzzle in the fewest number of steps possible. Ultimately, it involves constructing and reconstructing progressively larger ‘towers’, until the bottom disc can be moved to the third pole and the rest of the tower constructed upon it, as the text box explains in mathematical terms (See ‘Solving the Tower of Hanoi through recursion’ on the third page). The more discs that the puzzle contains, the more steps it will take – rising exponentially, in fact. This can be written in algebraic form: S = 2N-1
In this formula, S is the number of steps, and N is the number of discs. So, if the tower had five discs, the formula would be 25-1, which is 31. Therefore, solving the puzzle would take a minimum of 31 steps. If it had four discs, it would require only 15 steps – and for three discs, only 7.
Interestingly, this formula can lead us back to the Tower of Hanoi’s supposed mythological roots. The legend goes that young priests of a Hindu temple were tasked with moving discs of pure gold according to the rules of the puzzle – except that their Tower contained not 5 but 64 discs, and it was said that when they completed the task, the world would end. Using the formula above, we can deem that this is highly unlikely, given it would take them many billions of years to complete! Since this legend was invented by Lucas as a marketing ploy, it is hardly surprising that the underlying mathematics do not allow this apocalyptic prophecy to be put to the test.
GRAPHICAL REPRESENTATION
To visualise not only how many steps are needed, but exactly which steps too, the Tower of Hanoi configuration can be represented on a diagram that mathematicians call a graph. Graphs uncover aspects of a particular scenario that might have otherwise gone unseen, in particular by connecting them to other scenarios that may be better understood. “Many problems in discrete mathematics can be translated onto a graph, such as scenarios that involve flipping a switch or making a move in chess,” says Dan. “Once you have represented the problem this way, you can spot connections to other problems you already know about.”
This mode of thinking originated when mathematician Leonhard Euler was tasked with the ‘Seven Bridges of Königsberg’ challenge in 1736. Königsberg was a Prussian city bisected by a river that contained two large islands. The four areas between the islands and the two sides of the city were connected by seven bridges. Euler’s challenge was to find a route through the city that involved crossing all seven of the city’s bridges exactly once. He realised that the simplest way to approach the problem was to represent it as a graph, where lines (the bridges) connected four points (the banks and islands) in a way representative of the city’s actual layout. Once he had done this, he was able to easily demonstrate that the challenge was impossible. See the image on the right.
“The idea of representing collections of objects as graphs was a revolutionary one at the time it was invented, and remains incredibly useful,” says Dan. A similar simplification process can take place for the Tower of Hanoi. Any possible layout of the discs can be represented using a sequence of numbers. For instance, a Tower with three discs can be represented with a sequence of three numbers, going from the largest to smallest disc. The pole each disc is upon is represented by the value: pole 1, 2 or 3. For instance, the sequence ‘113’ means that the smallest disc is on the third pole and the two larger discs are on the first pole.
These sequences can be used to map out any possible steps from any position – for instance, from ‘111’ you can go to ‘112’ or ‘113’. These then branch out into other possibilities. It turns out that when all these possibilities are laid out, they can be represented in a very satisfying format – see the image below.
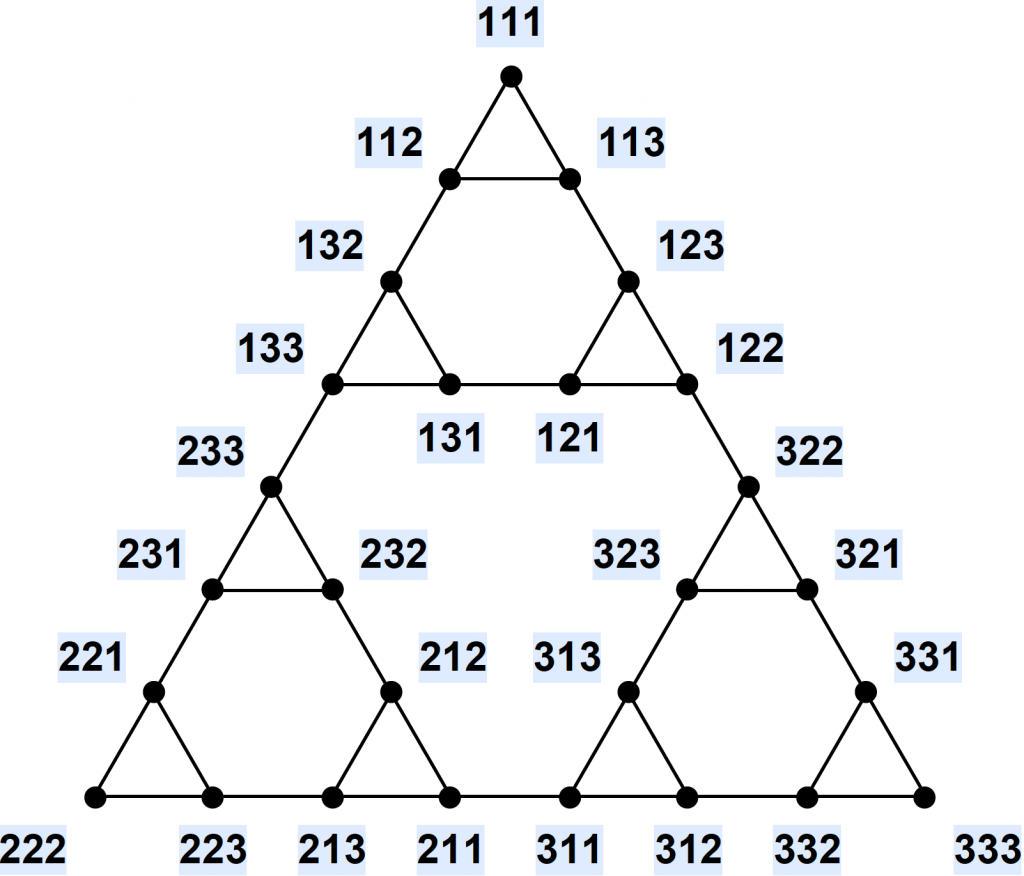
As well as being visually pleasing, this also makes it very easy to find the simplest way to complete the puzzle by finding the shortest route from ‘111’ to ‘333’. In fact, this logic can be applied to see how to get from one particular configuration to any other.
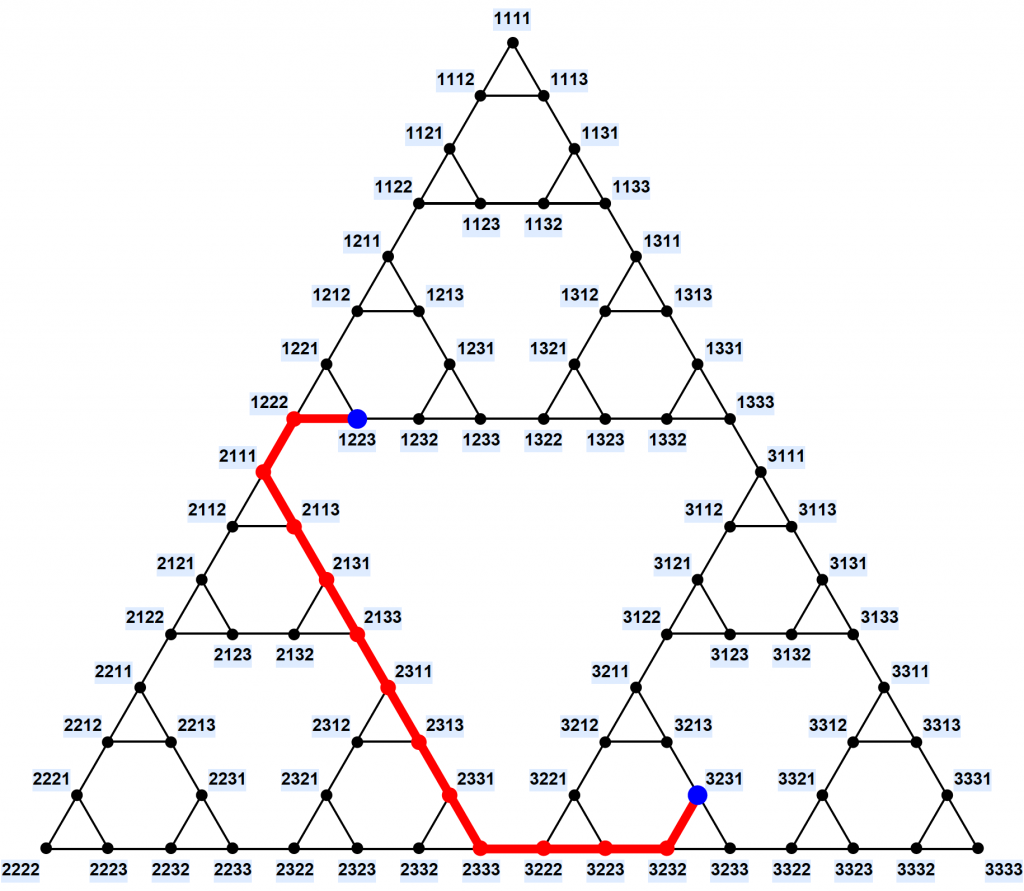
And there is more – because of the Tower’s underlying recursive structure, its associated graph is not just any simple graph, but is also a fractal. “The puzzle has turned out to be much more interesting than its inventor probably suspected,” says Dan.
FRACTALS
A fractal is a geometric shape that, loosely speaking, contains patterns that repeat themselves at many different scales. Fractals are often very appealing to the human eye and can be frequently found in nature – think about the branches of a tree, and how each is like a miniature tree with sub-branches of its own. Fractals are also a useful concept for solving mathematical problems. “Fractals often appear in mathematical problems where an object can be broken up into several pieces that are similar to but smaller than the original object,” says Dan.
The Tower of Hanoi is an elegant example of this fractal representation. Researchers in the 1980s noticed that when you graphically represent the steps within a Tower of Hanoi puzzle of any number of discs, you end up with something resembling a well-known fractal first described in 1915 for unrelated reasons: the Sierpiński triangle. You can see the resemblance for yourself below or in this animation, here:
http://math.ucdavis.edu/~romik/downloads/hanoi-animation.gif

“Mathematics is about discovering patterns in the world around us,” says Dan. “The most interesting sorts of patterns to discover are those that reveal that two concepts are related to each other, when beforehand no link between them we known. That’s when you know you’ve hit on a genuinely new idea.”
SHORTEST PATHS
Solving the Tower of Hanoi puzzle is tantamount to finding a shortest path in the graph between the ‘11…1’ state and the ‘33…3’ state. If someone hands you the puzzle after scrambling it to some weird configuration and asks you to bring it to some desired final state, you can do this by tracing out a shortest path in the graph between the sequences corresponding to the starting and ending states (see the figure below).
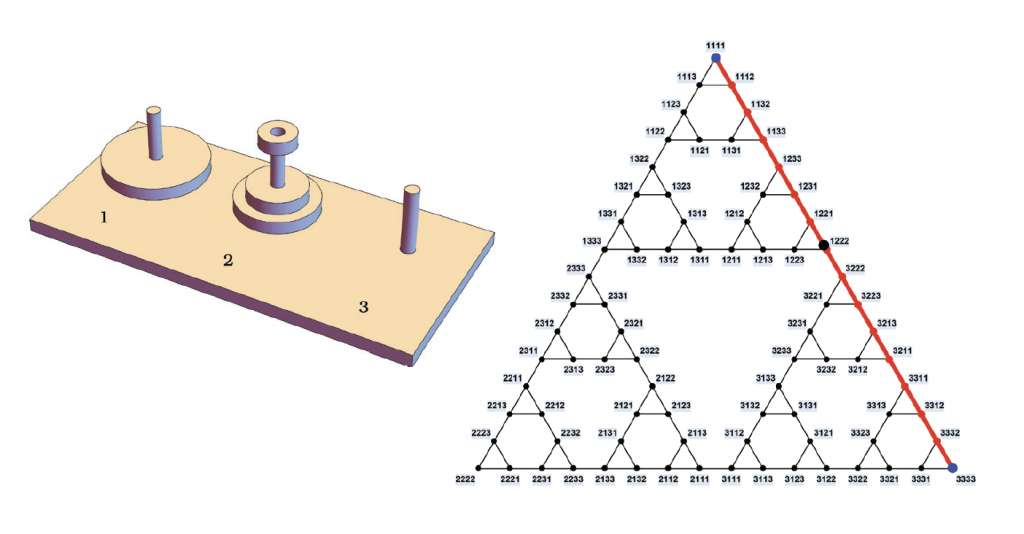
Dan’s inspiration to work on the Tower came after reading about the work of mathematician Andreas Hinz, who worked out a formula describing the average number of steps to get describing the average number of steps to get from one random configuration of the puzzle to another — that is, the average length of a shortest path connecting two random states of the puzzle. While in the worst possible case the number of steps would be 2N-1 (which happens when both the initial and final states happens when both the initial and final states have all the discs concentrated on one pole, as in the original problem), Hinz’s formula says that for general initial and final states, the number of steps required would be, on average, only 466/885 times 2N, or approximately 52.6% the number of steps of the worst case. (N is the number of discs).
“I was intrigued by the weirdness of Hinz’s formula and the appearance of the strange number 466/855 and decided to look at Hinz’s paper describing his ideas,” says Dan. “When I did and tried to understand his calculation, I realised I could improve on it in a small way and get a better understanding of where the number 466/885 comes from, and ended up writing my own paper on the subject. It was essentially a chance discovery driven by nothing more than curiosity.”
The idea of shortest paths is very satisfying, but what do these paths mean for the real world? “The Tower of Hanoi graph is a bit artificial to be of much practical use,” says Dan. “However, shortest paths in general are enormously important these days.” For instance, when we use SatNav, the SatNav’s software is literally finding a shortest path between two points in a graph. Shortest path algorithms are used by companies like UPS and Amazon to send packages in the most efficient way and by internet providers to route the text messages you send to your friends at a minimal cost – and in many other situations.
A GATEWAY TO MATHEMATICAL CONCEPTS
The Tower of Hanoi may not appear to have much real-world application, but it is beautiful, somewhat mysterious, and, as it happens, also acts as a gateway to a lot of extremely useful mathematical concepts – recursion, graphical representation and fractals among them. “Pure mathematics sometimes seems like it’s about the pursuit of knowledge that’s fun but useless, but it’s important to allow yourself to follow your curiosity,” says Dan. “There are many examples where major discoveries were made by mathematicians thinking about topics that might have appeared frivolous or self-indulgent. Following their curiosity meant that the world was made richer through cool discoveries.”
SOLVING THE TOWER OF HANOI THROUGH RECURSION
To move the N discs from pole A to pole B with the help of pole C, start by moving the top N-1 discs from pole A to pole C (the recursive bit that uses the same algorithm applied to a smaller number of discs; then move the largest disc from pole A to pole B; and then move the smallest N-1 discs from pole C to pole B (a second repetition of the recursive bit).
For an animation that shows this recursive solution in action, visit: https://www.math.ucdavis.edu/~romik/tower-of-hanoi/
 DAN ROMIK
DAN ROMIK
Professor
Department of Mathematics
University of California, Davis, USA
AREAS OF INTEREST: Combinatorics, Probability, Number Theory
 DAN ROMIK
DAN ROMIK Professor
Department of Mathematics
University of California, Davis, USA
AREAS OF INTEREST: Combinatorics, Probability, Number Theory
HOW TO BECOME A MATHEMATICIAN
• As well as academia, there are many organisations that offer mathematics-based apprenticeships or internships. Examples include Microsoft, NASA and MathWorks.
• According to Indeed, the average annual salary for a mathematician in the US is around $93k.
Unsurprisingly, mathematics (and further mathematics, if available) is the most useful subject to study at school to go on to a degree in mathematics. Other useful subjects are physics, chemistry, biology and computer programming. While not generally required, also taking a humanities subject can help broaden your skillset.
A degree in mathematics can open doors to a huge and growing range of careers. Many computer programmers, analysts, economists, software developers and data scientists come from mathematical backgrounds, to name a few.
Write it in the comments box below and Dan will get back to you. (Remember, researchers are very busy people, so you may have to wait a few days.)





Dear Professor Romik,
I have just enjoyed reading your article about the Tower of Hanoi.
I am coordinator of a non-profit group named Upcycling Club 1 in Palmerston North, New Zealand. Under the slogan of “Creative Conservation” we aim to make and play with items made out of pre-loved and recycled materials. We offer regular free arts and craft workshops at our city museum, Museum of Arts, Science and History.
One of the most popular activities we do is the Tower of Hanoi. We make kits of Tower of Hanoi using hard covers of unwanted books from Red Cross book sales for bases, and bottle tops/jar lids for discs. We make bags out of fabric remnants and recycled clothing.
We are now working on instruction sheets to accompany the kits. They will be 2 pages long, but on request a 6 page (or so) version will be sent on request separately. Further a modified version will be submitted to the online publisher Frontiers in the near future.
Here is the reason why I am writing this mail to you. Would you give us your permission to quote your “Pathway from school to mathematician”, please? Main readers of my paper for Frontiers will be older children, so your statement is
just spot on. On another occasion I would also like to write about scholars whose interests in their chosen fields began when they were children.
Thank you and kind regards, Yoko Wakiya
Dear Yoko,
Thank you for the nice feedback about the article. It’s fantastic that you and your group are making Tower of Hanoi kits out of recycled materials! About your question, the article was published by Futurum with the same kind of recyclability in mind, so everyone is free to use or even adapt the materials, subject only to mild conditions of attribution of the source and noncommercial use. Specifically, if you’ll look at the bottom of this web page you should see a notice that “All Futurum content is produced, created and published under the Creative Commons license: Attribution-NonCommercial 4.0 International (CC BY-NC 4.0).” The link to the license if you want to learn more is https://creativecommons.org/licenses/by-nc/4.0/ . So, quoting with appropriate credit is certainly fine.
Hope this helps!
–Dan
Dear Professor Romik,
Is there a way to solve the Tower of Hanoi puzzle using permutations and combinations? I’ve been trying to research whether or not it can be solved and I have not had much luck. Do you have any ideas?
Yes it can be solved, but not specifically using permutations and combinations as far as I’m aware. The book The Tower of Hanoi — Maths and Myths, by Hinz, Klavzar, Milutinovic and Petr is a good reference if you want to know what’s been done.
Answer the following questions: You may use bullets in organizing your answers.
Instruction: With the Recurrence Relations topic, it consists of 3 modeling namely: Fibonacci Numbers, The Tower of Hanoi and Counting Problem. Discuss each in a simplest way and give at least one (1) example each with proper explanation.
PLEASE HELP!!!
Hi Christian,
Thank you for your message. We cannot ask Dan to do your homework for you and therefore suggest that you ask your teacher for help with this. If you read Dan’s article, you will be able to explain the Tower of Hanoi in simple terms.
Wishing you all the very best,
The Futurum team
This is a very helpful article… thanks!!! I have one editorial suggestion: The 4-disk graph just underneath the 3-disk solution appears to be labeled incorrectly – it is full of invalid transitions from one vertex to the next, i.e., transitions that involve moving more than one disk at a time. (Perhaps it is intended to represent something other than the Tower of Hanoi puzzle, but it is not clear what that something other might be.) The article goes on to introduce fractals, and the 4-disk graph is then shown again, this time with vertex labels that indicate valid transitions per the Hanoi puzzle.
I noticed what Steve Baker mentioned too.