Spreading the joy of mathematics
Dr James Tanton is the founder of the Global Math Project, a worldwide movement of teachers committed to inspiring a love of mathematics in students and spreading the joy of this amazing subject to all corners of the globe!
Following tried and tested methods can be the right course of action for some people, but not Dr James Tanton. James is the founder of the Global Math Project, an exciting worldwide movement of teachers and educators taking a new and innovative approach to inspiring a love of mathematics in students.
WHAT WAS JAMES’ PERSONAL MOTIVATION FOR THE PROJECT?
James grew up in Australia where he enjoyed school very much. However, when it came to learning maths, he found that the process was extremely rigid and traditional; from an early age, he came to see that his purpose in a maths class was to memorise what he was told, then repeat it. However, he had (and continues to have) a natural curiosity and a desire to ask questions, rather than parrot answers he has been given. One formative moment occurred when he was 13. “Our teacher began by asking the class to take out our rulers and protractors, draw three examples of right-angled triangles, measure each of their three side lengths, and compute a2 + b2 and compare it with c2 to see they have the same value,” recalls James. “I had two problems with the exercise. The first was that I did not believe anyone was seeing a2 + b2 equalling c2: no human can measure exactly enough to see them be absolutely equal. I let this issue slide. Everyone thought it turned out to be close enough to be believed. But I could not let my second issue slide.”
James decided to ask the teacher a question: was it possible to know why the value of c2 being the same as a2 + b2 was not just a coincidence? The teacher told James to repeat the task, expecting that seeing another three examples would turn it from coincidence to mathematical fact. James was being asked to tread the same path that had gone before without questioning it. He came to realise that his teacher was not in the position to help his pupils understand why something was the case – it was enough for them to simply know that it was.
This experience stirred something within James that continued to grow over the years: the desire to ensure no one is denied the opportunity to see the awe, wonder and profound joy that mathematics can offer.
HOW DID JAMES BUILD A WORLDWIDE MATHS COMMUNITY?
It began with an idea that relied on the kindness of people and volunteers to make it a reality. “Teachers are the most wonderful advocates of mathematics and they have come through in spades to get this grass-roots effort off the ground,” says James. “The fact that we have reached over 6.4 million students from across 170 countries and territories solely by word-of-mouth and basic social media is truly remarkable. Astounding, in fact! And this is mathematics – classroom mathematics!”
The Global Math Ambassadors involved are people with a range of backgrounds and experiences who have discovered the Global Math Project and have pledged to help spread the wonder of mathematics.
WHAT IS GLOBAL MATH WEEK?
James, and his six co-founders, felt it was a good idea to pick some dates that could serve as Global Math Week. Somewhat ironically, given the thinking behind the project, they decided on 10 – 17 October, which is eight days! Whether you write the date in DD/MM format or MM/ DD format, the start date will always be 10/10, so everyone around the world can remember it.
The first Global Math Week took place in 2017 – “We simply asked teachers across the planet to conduct just one Exploding Dots lesson sometime during the week and let the world know by making a comment about it on social media,” explains James. “By the end of that week, we had 1.7 million students and teachers try out Exploding Dots on the web app, and we know that many others conducted lessons in their classrooms without technology.”
Of course, the pandemic that continues to wreak havoc around the world impacted on Global Math Week 2020, but the team collaborated with the National Museum of Mathematics to offer a series of lessons to people around the world. In addition, they worked with the Mathematical Association of America to offer an open series of activities entitled ‘Puzzles that can be Explained with Exploding Dots’.
WHAT IS EXPLODING DOTS?
Put simply, Exploding Dots is an exciting and successful technique that teachers can use in the classroom to encourage and inspire maths students. It is a story that comes in 12 short-and-swift explorations that act as a purely visual way to cut through the clutter and literally see the meaning and operations of place-value and arithmetic. “It overcomes barriers of language and even choice of base,” explains James. “Humans have a predilection for the number 10 when we count and do arithmetic because of how many fingers we have, but there may well be people around the world who want to use a different base to 10. We cater for that!”
The idea behind Exploding Dots is to provide students with an intuitive understanding of place value, which then ensures that more maths, such as polynomial algebra and infinite series, falls into place. Students readily go from the basic maths of how we write and think about numbers, through all the arithmetic one learns in primary school, to high-school algebra and pre-calculus, all the way up to some unsolved problems that still baffle mathematicians to this day.
HAS JAMES FACED ANY CHALLENGES WITH THE PROJECT?
Yes. Unfortunately, there will always be those who are sceptical of something new. Several maths teachers have told James that they have had to conduct Exploding Dots with their students semi-secretly. “There is a lot of pressure on teachers to only teach endorsed curriculum content that is immediately tied to current curriculum standards. Since the story of Exploding Dots starts with mathematics from the early grades and moves its way through the entire K-12 curriculum, we can give the full story of the subject and not be pigeon-holed into just doing content relevant to year 5 or year 10,” says James. “Initially, we were at odds with many school administrators’ views that classroom maths should always – and only ever – be connected to the maths of that grade level. The idea of putting that mathematics in full context did not seem to be a priority.”
Reference
https://doi.org/10.33424/FUTURUM116
WHAT WAS JAMES’ PERSONAL MOTIVATION FOR THE PROJECT?
James grew up in Australia where he enjoyed school very much. However, when it came to learning maths, he found that the process was extremely rigid and traditional; from an early age, he came to see that his purpose in a maths class was to memorise what he was told, then repeat it. However, he had (and continues to have) a natural curiosity and a desire to ask questions, rather than parrot answers he has been given. One formative moment occurred when he was 13. “Our teacher began by asking the class to take out our rulers and protractors, draw three examples of right-angled triangles, measure each of their three side lengths, and compute a2 + b2 and compare it with c2 to see they have the same value,” recalls James. “I had two problems with the exercise. The first was that I did not believe anyone was seeing a2 + b2 equalling c2: no human can measure exactly enough to see them be absolutely equal. I let this issue slide. Everyone thought it turned out to be close enough to be believed. But I could not let my second issue slide.”
James decided to ask the teacher a question: was it possible to know why the value of c2 being the same as a2 + b2 was not just a coincidence? The teacher told James to repeat the task, expecting that seeing another three examples would turn it from coincidence to mathematical fact. James was being asked to tread the same path that had gone before without questioning it. He came to realise that his teacher was not in the position to help his pupils understand why something was the case – it was enough for them to simply know that it was.
This experience stirred something within James that continued to grow over the years: the desire to ensure no one is denied the opportunity to see the awe, wonder and profound joy that mathematics can offer.
HOW DID JAMES BUILD A WORLDWIDE MATHS COMMUNITY?
It began with an idea that relied on the kindness of people and volunteers to make it a reality. “Teachers are the most wonderful advocates of mathematics and they have come through in spades to get this grass-roots effort off the ground,” says James. “The fact that we have reached over 6.4 million students from across 170 countries and territories solely by word-of-mouth and basic social media is truly remarkable. Astounding, in fact! And this is mathematics – classroom mathematics!”
The Global Math Ambassadors involved are people with a range of backgrounds and experiences who have discovered the Global Math Project and have pledged to help spread the wonder of mathematics.
WHAT IS GLOBAL MATH WEEK?
James, and his six cofounders, felt it was a good idea to pick some dates that could serve as Global Math Week. Somewhat ironically, given the thinking behind the project, they decided on 10 – 17 October, which is eight days! Whether you write the date in DD/MM format or MM/ DD format, the start date will always be 10/10, so everyone around the world can remember it.
The first Global Math Week took place in 2017 – “We simply asked teachers across the planet to conduct just one Exploding Dots lesson sometime during the week and let the world know by making a comment about it on social media,” explains James. “By the end of that week, we had 1.7 million students and teachers try out Exploding Dots on the web app, and we know that many others conducted lessons in their classrooms without technology.”
Of course, the pandemic that continues to wreak havoc around the world impacted on Global Math Week 2020, but the team collaborated with the National Museum of Mathematics to offer a series of lessons to people around the world. In addition, they worked with the Mathematical Association of America to offer an open series of activities entitled ‘Puzzles that can be Explained with Exploding Dots’.
WHAT IS EXPLODING DOTS?
Put simply, Exploding Dots is an exciting and successful technique that teachers can use in the classroom to encourage and inspire maths students. It is a story that comes in 12 short-and-swift explorations that act as a purely visual way to cut through the clutter and literally see the meaning and operations of place-value and arithmetic. “It overcomes barriers of language and even choice of base,” explains James. “Humans have a predilection for the number 10 when we count and do arithmetic because of how many fingers we have, but there may well be people around the world who want to use a different base to 10. We cater for that!”
The idea behind Exploding Dots is to provide students with an intuitive understanding of place value, which then ensures that more maths, such as polynomial algebra and infinite series, falls into place. Students readily go from the basic maths of how we write and think about numbers, through all the arithmetic one learns in primary school, to high-school algebra and pre-calculus, all the way up to some unsolved problems that still baffle mathematicians to this day.
HAS JAMES FACED ANY CHALLENGES WITH THE PROJECT?
Yes. Unfortunately, there will always be those who are sceptical of something new. Several maths teachers have told James that they have had to conduct Exploding Dots with their students semi-secretly. “There is a lot of pressure on teachers to only teach endorsed curriculum content that is immediately tied to current curriculum standards. Since the story of Exploding Dots starts with mathematics from the early grades and moves its way through the entire K-12 curriculum, we can give the full story of the subject and not be pigeon-holed into just doing content relevant to year 5 or year 10,” says James. “Initially, we were at odds with many school administrators’ views that classroom maths should always – and only ever – be connected to the maths of that grade level. The idea of putting that mathematics in full context did not seem to be a priority.”
However, times are changing. Increasingly, James and the team are invited to give live online sessions to students in schools across the US and curriculum writers are asking for permission to use Exploding Dots in their materials. As with many grassroot efforts, a major challenge is funding. The project relies on volunteer effort, but it is important to try and compensate people for their time and effort. James explains, “We would like to translate all our materials into as many languages as possible, for instance, and develop more curriculum materials.”
WHERE DOES JAMES SEE THE PROJECT HEADING?
While Global Math Week is an extremely important part of what James and the team are trying to achieve, the truth is that the maths they offer is year-long. Thus, there is an emphasis on live classroom lessons and the materials that are used to teach them. “We are becoming a classroom presence in North America and I can only see that strengthening and expanding around the globe in the future,” says James. “We also offer other topics and hope to see them gain increased awareness and popularity in the future. In fact – we would love to offer versions of all the maths presented in K-12 schools in joyous ways. There is nothing wrong with thinking big!”
 DR JAMES TANTON
DR JAMES TANTON
Mathematician-at-Large for the Mathematical Association of America, Founder of the Global Math Project, educator and author.
FIELD OF INTEREST: Mathematics Education and Outreach
RESEARCH PROJECT: James is the founder of the Global Math Project which is an exciting initiative designed to inspire a love for mathematics in students. The flagship programme within the project is Exploding Dots, a visual means of understanding maths that speaks a universal language.
SUPPORTER: The American Institute of Mathematics
HOW DID JAMES BECOME A MATHEMATICIAN?
“I was a bit of a lonely child. I remember spending long periods of time staring at my bedroom ceiling and thinking about maths puzzles. I have actually produced an essay detailing my favourite maths puzzle which came about because my childhood bedroom had a particularly geometric pattern. I began inventing puzzles and games based on that grid.
I also liked to imagine what it would take to talk with aliens (again, I have produced an essay that explains this in more detail). As you can see, my main interest as a child was maths – it has been in my mind for as long as I can remember and I am as passionate about it now as I was then, if not more.
I think my curiosity has been a great asset, as has my confidence to always think of the why, what else and what if questions. Behind that is a willingness to tinker and play with ideas, which is key to being a mathematician. My schoolwork was always about getting numerical answers to questions and then stopping. In my opinion, the answers are the boring part! How to get an answer is far more interesting, and then changing the path one took to get to an answer to see what new insights doing so could offer is the extra fun.
I am willing to ‘walk into the haze’. We all know when studying a subject that there are hazy parts where you secretly know you don’t quite get what is going on, or you sense something hasn’t quite clicked, but you can still do the work and push on. These parts can be a bit scary and most people tend to push them out of their mind. My schooling encouraged this, but I have since learned not to be afraid of the haze and instead recognise it as the place to go to find deep understanding and meaning. The haze is a signal that something is amiss, so explore this. Find all those fabulous lightbulbs in your mind and switch them on!
My proudest career achievement was at 11am on day two of our first Global Math Week when I was sitting at my laptop and saw the counter on our Exploding Dots site turn to one million! This made me cry. I had no idea that our hare-brained attempt to bring a piece of joyous school-connected mathematics to the world would be noticed and accepted.
My ambition is to change the entire world’s perception of what mathematics can and should be. I am not hoping for everyone to love mathematics, but I do want everyone to see that there is something to love about it, to understand why others love it, and to know that mathematics is within their reach if they wanted to pursue it. I want it to be their choice!”
HOW TO BECOME A MATHEMATICIAN
• The American Institute of Mathematics, a supporter of James’s project, is a brilliant resource for those interested in all things maths: https://aimath.org
• The Mathematical Association of America provides maths-related news, programmes and communities to help you get involved: https://www.maa.org/
• According to www.salary.com, the salary for a mathematician in the US typically falls into the range of $64,000 to $98,000, although it depends massively on the level of experience, whether you are an academic or professional, and what your specific area of maths is.
PATHWAY FROM SCHOOL TO MATHEMATICS
It goes without saying that you will need to study maths at GCSE and A level (or equivalent). However, physics is also useful, while there are those students who choose to take other subjects as well, including IT and computing, chemistry and business studies.
You will need a degree in a relevant subject for postgraduate study.
www.theuniguide.co.uk/advice/a-level-choices/what-a-levels-doyou-need-to-study-maths
JAMES’ TOP TIPS FOR STUDENTS
01 If you are struggling to find the joy in maths, then do your best to work through the clutter in your mind and try to understand the process. Many students will merely memorise stuff they have learned, but the joy comes from developing genuine understanding.
02 The internet is a truly wonderful source for finding out about the stories behind mathematics. It is easy to find yourself down some fun rabbit holes and encounter some amazing maths along the way!
03 Reflect on the parts of maths that are hazy in your mind and consider what it is that is proving difficult. It sometimes helps to take a step back and ask questions. Can you truly explain why negative multiplied by negative is positive? Why did mathematicians switch from degrees to radians for advanced maths? Maths is as much about asking questions than it is providing answers.
JAMES’ TOP TIPS FOR TEACHERS
01 Try de-emphasising the focus on getting answers and focus more on the processes involved. Perhaps, try giving tests with all the numerical answers given in the margin but with blank spaces for students to write out their work.
02 Tell the stories of mathematics. Hunt the internet for the history of the mathematics at hand. Why are quadratic equations called ‘quadratic’ when the prefix quad means four? Who chose the number 360 for the count of degrees in a circle? Why isn’t December the tenth month of the year when deca means ten? Look up the quirky names of the common math symbols we use: obelus, vinculum, radix, virgul, and so on. Better yet – have students look things up and tell you!
03 Talk about the nature of problem-solving with your students. Reacting in human ways is perfectly normal, so when your class is stuck on a tough problem, make their homework something like, “Go for a 20-minute walk and do not think about this maths problem.” Someone always comes back the next day with new insight!
Do you have a question for James?
Write it in the comments box below and James will get back to you. (Remember, researchers are very busy people, so you may have to wait a few days.)





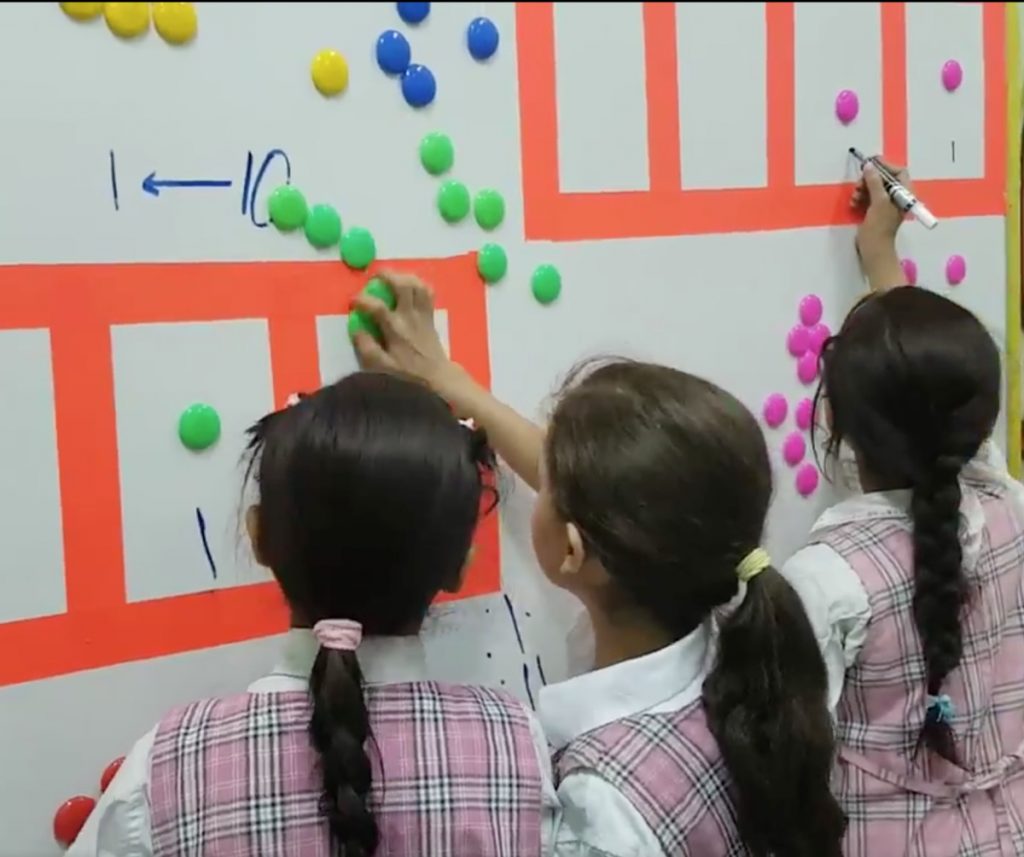





Dr. Tanton,
A couple of years ago I asked you a question about calculating square roots. You asked me to explain my technique for doing sos. Unfortunately I never got around to responding. My question was “can you use my technique using Exploding Dots”?
Sqrt(2)= (try 1), square both sides. If the right side is smaller than the left side then increment it and repeat. When the right side is equal to or greater than the left side, then go back one step, go to the next decimal digit and repeat the process ad infinititum.